Uma variável aleatória é uma função que associa um número real a cada resultado possível de um experimento aleatório. Este conceito é fundamental em probabilidade e estatística, permitindo a análise matemática de fenômenos aleatórios.
Elas são a base para entender distribuições de probabilidade e fazer inferências estatísticas.
1. Tipos de Variáveis Aleatórias
1.1 Variáveis Aleatórias Discretas
São aquelas que assumem valores em um conjunto enumerável (finito ou infinito contável).
Características
- Valores isolados
- Podem ser contados
- Representadas por função de probabilidade
Exemplos
- Número de faces em um dado
- Quantidade de clientes em uma fila
- Número de defeitos em um lote
Lançamento de um dado: X = número que aparece na face superior
Valores possíveis: {1, 2, 3, 4, 5, 6}
1.2 Variáveis Aleatórias Contínuas
São aquelas que assumem valores em um intervalo dos números reais.
Características
- Valores em um intervalo contínuo
- Não podem ser contados, apenas medidos
- Representadas por função densidade de probabilidade
Exemplos
- Altura de uma pessoa
- Tempo de espera em um serviço
- Temperatura em um dia
Temperatura diária: X = temperatura em graus Celsius
Valores possíveis: [0°C, 40°C]
2. Funções de Probabilidade
2.1 Função de Probabilidade (Caso Discreto)
Definição
Uma função $p(x)$ é uma função de probabilidade se:
- $p(x) \geq 0$ para todo $x$
- $\sum_{x} p(x) = 1$
- $P(X = x) = p(x)$
Exemplo
Para um dado justo: \(p(x) = \frac{1}{6}, \text{ para } x \in \{1,2,3,4,5,6\}\)
2.2 Função Densidade de Probabilidade (Caso Contínuo)
Definição
Uma função $f(x)$ é uma função densidade de probabilidade se:
- $f(x) \geq 0$ para todo $x$
- $\int_{-\infty}^{\infty} f(x)dx = 1$
- $P(a \leq X \leq b) = \int_{a}^{b} f(x)dx$
Em variáveis aleatórias contínuas, a probabilidade de um valor específico é sempre zero: $P(X = x) = 0$
3. Esperança e Variância
3.1 Esperança (Valor Esperado)
Caso Discreto
Para um dado justo (faces de 1 a 6), onde todas as probabilidades são iguais:
\[E[X] = \sum_{i=1}^{6} x_i \cdot P(x_i) = \frac{1 + 2 + 3 + 4 + 5 + 6}{6} = 3.5\]using Statistics
# Exemplo: Lançamento de um dado
valores = 1:6
probabilidades = fill(1/6, 6) # Probabilidades iguais para cada face
# Calculando a esperança
esperanca = sum(valores .* probabilidades)
println("Esperança (média) do lançamento do dado: ", esperanca)
# Simulando lançamentos
n_lancamentos = 10000
lancamentos = rand(1:6, n_lancamentos)
media_empirica = mean(lancamentos)
println("\nMédia empírica após $n_lancamentos lançamentos: ", media_empirica)Caso Contínuo
Para uma distribuição Normal com média μ e desvio padrão σ:
\[E[X] = \mu = \int_{-\infty}^{\infty} x \cdot \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx\]Para μ = 10 e σ = 2:
\[E[X] = \int_{-\infty}^{\infty} x \cdot \frac{1}{\sqrt{2\pi(2)^2}} e^{-\frac{(x-10)^2}{2(2)^2}} dx\] \[E[X] = \int_{-\infty}^{\infty} x \cdot \frac{1}{\sqrt{8\pi}} e^{-\frac{(x-10)^2}{8}} dx\] \[E[X] = \mu = 10\]A integral é resolvida através de: - Mudança de variável: y = (x-μ)/σ - Simetria da distribuição normal - Propriedades de funções pares e ímpares
No exemplo em Julia, usamos μ = 10 e σ = 2.
using Distributions, Statistics
# Exemplo: Distribuição Normal
μ = 10 # média
σ = 2 # desvio padrão
dist = Normal(μ, σ)
# Valor esperado teórico
esperanca_teorica = mean(dist)
println("Esperança teórica: ", esperanca_teorica)
# Simulação
n_amostras = 10000
amostras = rand(dist, n_amostras)
media_empirica = mean(amostras)
println("\nMédia empírica após $n_amostras amostras: ", media_empirica)3.2 Variância
Definição
\(Var(X) = E[(X - E(X))^2] = E(X^2) - [E(X)]^2\)
Caso Discreto (Dado)
Para um dado justo:
\[Var(X) = E[(X - E[X])^2] = \sum_{i=1}^{6} (x_i - 3.5)^2 \cdot \frac{1}{6} = \frac{35}{12} \approx 2.917\]Caso Contínuo (Normal)
Para uma distribuição Normal:
\[Var(X) = \sigma^2 = \int_{-\infty}^{\infty} (x - \mu)^2 \cdot \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx\]using Statistics, Distributions
# Exemplo com dado (caso discreto)
valores = 1:6
probabilidades = fill(1/6, 6)
# Calculando variância teórica
media = sum(valores .* probabilidades)
variancia_teorica = sum((valores .- media).^2 .* probabilidades)
println("Variância teórica do dado: ", variancia_teorica)
# Simulação
n_lancamentos = 10000
lancamentos = rand(1:6, n_lancamentos)
variancia_empirica = var(lancamentos)
println("\nVariância empírica após $n_lancamentos lançamentos: ", variancia_empirica)
# Exemplo com distribuição normal (caso contínuo)
dist_normal = Normal(10, 2)
println("\nVariância teórica da Normal(10,2): ", var(dist_normal))
amostras_normal = rand(dist_normal, n_lancamentos)
println("Variância empírica das amostras normais: ", var(amostras_normal))A variância mede a dispersão dos valores em torno da média. Quanto maior a variância, mais dispersos estão os valores.
4. Funções de Variáveis Aleatórias
4.1 Transformações
Se Y = g(X), onde g é uma função e X é uma variável aleatória:
Para Discretas
\(P(Y = y) = \sum_{x: g(x)=y} P(X = x)\)
Para Contínuas
\(f_Y(y) = f_X(g^{-1}(y)) \cdot |\frac{d}{dy}g^{-1}(y)|\)
Para Y = X², onde X ~ N(0,1):
1) Densidade da Normal padrão (variável original X): \(f_X(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2}, \quad -\infty < x < \infty\)
2) Função de transformação: \(g(x) = x^2\)
3) Função inversa (dois ramos devido ao quadrado): \(g^{-1}(y) = \pm\sqrt{y}, \quad y \geq 0\)
4) Derivada da função inversa: \(\frac{d}{dy}g^{-1}(y) = \pm\frac{1}{2\sqrt{y}}\)
5) Valor absoluto da derivada: \(|\frac{d}{dy}g^{-1}(y)| = \frac{1}{2\sqrt{y}}\)
6) Aplicando a fórmula de transformação para ambos os ramos: \(f_Y(y) = f_X(\sqrt{y}) \cdot \frac{1}{2\sqrt{y}} + f_X(-\sqrt{y}) \cdot \frac{1}{2\sqrt{y}}\)
7) Substituindo a densidade da normal: \(f_Y(y) = \frac{1}{\sqrt{2\pi}} e^{-(\sqrt{y})^2/2} \cdot \frac{1}{2\sqrt{y}} + \frac{1}{\sqrt{2\pi}} e^{-(-\sqrt{y})^2/2} \cdot \frac{1}{2\sqrt{y}}\)
8) Simplificando a exponencial: \(f_Y(y) = \frac{1}{\sqrt{2\pi}} e^{-y/2} \cdot \frac{1}{2\sqrt{y}} + \frac{1}{\sqrt{2\pi}} e^{-y/2} \cdot \frac{1}{2\sqrt{y}}\)
9) Combinando os termos: \(f_Y(y) = \frac{1}{\sqrt{2\pi}} e^{-y/2} \cdot \frac{1}{\sqrt{y}} = \frac{1}{\sqrt{2\pi y}} e^{-y/2}, \quad y > 0\)
10) Cálculo da Esperança: \(E[Y] = E[X^2] = Var(X) + [E(X)]^2 = 1 + 0^2 = 1\)
11) Cálculo da Variância: \(E[Y^2] = E[X^4] = 3\) \(Var(Y) = E[Y^2] - (E[Y])^2 = 3 - 1^2 = 2\)
A distribuição resultante Y é conhecida como qui-quadrado com 1 grau de liberdade (χ²(1)). Esta transformação é fundamental em testes de hipóteses e intervalos de confiança.
using Distributions, Plots
# Exemplo: Transformação de uma variável aleatória normal
X = Normal(0, 1) # Distribuição normal padrão
n_amostras = 10000
# Gerando amostras de X
amostras_x = rand(X, n_amostras)
# Transformação Y = X² (qui-quadrado com 1 grau de liberdade)
amostras_y = amostras_x.^2
# Plotando histogramas
x_vals = -4:0.01:4 # Intervalo para a PDF teórica
p1 = histogram(amostras_x,
bins=50,
normalize=:pdf,
title="X ~ Normal(0,1)",
label="Amostras",
color=:steelblue,
lw=0,
alpha=0.6)
plot!(p1, x_vals, pdf.(X, x_vals), lw=2, color=:darkred, label="PDF teórica")
p2 = histogram(amostras_y,
bins=50,
normalize=:pdf,
title="Y = X² ~ χ²(1)",
label="Amostras",
color=:steelblue,
lw=0,
alpha=0.6)
# Plotando os dois gráficos lado a lado
plot(p1, p2, layout=(1,2), size=(800,400))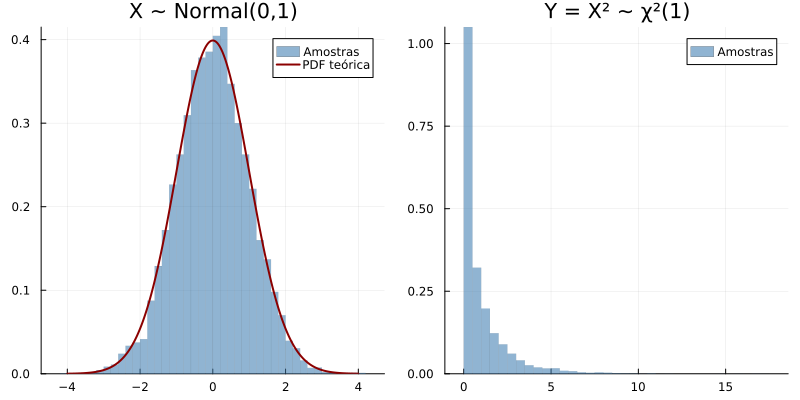
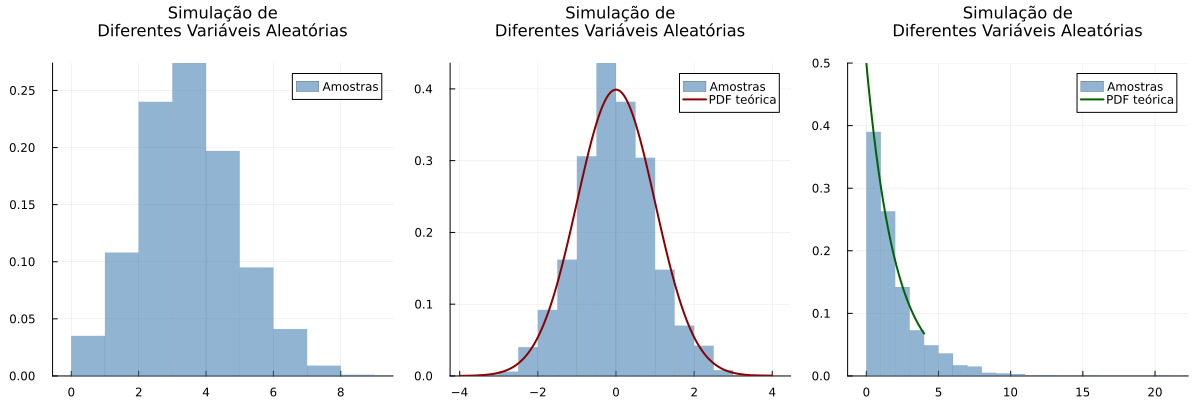
4.2 Simulação de Variáveis Aleatórias
Binomial(n,p)
Função de probabilidade:
\[P(X = k) = \binom{n}{k}p^k(1-p)^{n-k}, \quad k = 0,1,...,n\]Para n = 10 e p = 0.3:
\[P(X = k) = \binom{10}{k}(0.3)^k(0.7)^{10-k}\] \[E[X] = np = 10 \cdot 0.3 = 3\] \[Var(X) = np(1-p) = 10 \cdot 0.3 \cdot 0.7 = 2.1\]Normal(μ,σ)
Função densidade de probabilidade:
\[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]Para μ = 0 e σ = 1:
\[f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}\] \[E[X] = \mu = 0\] \[Var(X) = \sigma^2 = 1\]Exponencial(λ)
Função densidade de probabilidade:
\[f(x) = \lambda e^{-\lambda x}, \quad x \geq 0\]Para λ = 2:
\[f(x) = 2e^{-2x}, \quad x \geq 0\] \[E[X] = \frac{1}{\lambda} = \frac{1}{2}\] \[Var(X) = \frac{1}{\lambda^2} = \frac{1}{4}\]using Distributions, Plots, Random
using Measures
# Fixando a semente para reprodutibilidade
Random.seed!(123)
# Simulando diferentes tipos de variáveis aleatórias
n_amostras = 1000
# 1. Discreta: Binomial
X_bin = Binomial(10, 0.3)
amostras_bin = rand(X_bin, n_amostras)
# 2. Contínua: Normal
X_norm = Normal(0, 1)
amostras_norm = rand(X_norm, n_amostras)
# 3. Contínua: Exponencial
X_exp = Exponential(2)
amostras_exp = rand(X_exp, n_amostras)
# Criando subplots
p1 = histogram(amostras_bin,
bins=11,
normalize=:probability,
color=:steelblue,
alpha=0.6,
lw=0,
title="Binomial(10, 0.3)",
label="Amostras")
x_vals_norm = -4:0.01:4
p2 = histogram(amostras_norm,
bins=30,
normalize=:pdf,
color=:steelblue,
alpha=0.6,
lw=0,
title="Normal(0, 1)",
label="Amostras")
plot!(p2, x_vals_norm, pdf.(X_norm, x_vals_norm), lw=2, color=:darkred, label="PDF teórica")
x_vals_exp = 0:0.01:4
p3 = histogram(amostras_exp,
bins=30,
normalize=:pdf,
color=:steelblue,
alpha=0.6,
lw=0,
title="Exponencial(2)",
label="Amostras")
plot!(p3, x_vals_exp, pdf.(X_exp, x_vals_exp), lw=2, color=:darkgreen, label="PDF teórica")
# Combinando os plots
plot(p1, p2, p3,
layout=(1,3),
size=(1200,400),
title="Simulação de\nDiferentes Variáveis Aleatórias",
titlefontsize=11,
top_margin=10mm
)
5. Aplicações Práticas
Engenharia
- Controle de qualidade
- Análise de confiabilidade
- Processamento de sinais
Finanças
- Análise de risco
- Precificação de ativos
- Gestão de portfólio
Ciências Naturais
- Mecânica quântica
- Genética
- Ecologia populacional
Computação
- Machine Learning
- Simulações
- Análise de algoritmos
Em machine learning, variáveis aleatórias são usadas para modelar incertezas e fazer previsões probabilísticas.
Referências
- Ross, S. M. Introduction to Probability Models. 12ª ed. Academic Press, 2019.
- Papoulis, A.; Pillai, S. U. Probability, Random Variables and Stochastic Processes. 4ª ed. McGraw-Hill, 2002.
- Feller, W. An Introduction to Probability Theory and Its Applications. Vol. 1, 3ª ed. Wiley, 1968.
- DeGroot, M. H.; Schervish, M. J. Probability and Statistics. 4ª ed. Pearson, 2012.
- Mood, A. M.; Graybill, F. A.; Boes, D. C. Introduction to the Theory of Statistics. 3ª ed. McGraw-Hill, 1974.
