Probabilidade Condicional

A Probabilidade Condicional é um conceito fundamental que nos permite calcular a probabilidade de um evento ocorrer, dado que outro evento já ocorreu. Este conceito é essencial para entender dependência entre eventos e fazer previsões mais precisas.

🎯 Importante:
A probabilidade condicional de um evento $$A$$ dado que $$B$$ ocorreu é denotada por $$P(A\mid B)$$ e é calculada como: $$P(A\mid B) = \frac{P(A \cap B)}{P(B)}, \text{ onde } P(B) > 0$$

1. Definição e Conceitos Básicos

1.1 Definição Formal

A probabilidade condicional $P(A\mid B)$ representa a probabilidade de ocorrência do evento $A$, sabendo que o evento $B$ já ocorreu. Formalmente:

\[P(A\mid B) = \frac{P(A \cap B)}{P(B)}, \text{ onde } P(B) > 0\]

1.2 Interpretação Geométrica

A probabilidade condicional pode ser visualizada como uma restrição do espaço amostral original ao evento condicionante:

julia

using Plots

# Função para criar círculo
function circle(h, k, r)
    θ = range(0, 2π, length=100)
    h .+ r*cos.(θ), k .+ r*sin.(θ)
end

# Plot base
plot(size=(800,400), layout=(1,2), legend=:topright)

# Espaço amostral original
p1 = plot!(subplot=1, title="Eventos A e B")
plot!(p1, circle(0,0,1), seriestype=:shape, alpha=0.3, color=:gray, label="Ω")
plot!(p1, circle(-0.3,0,0.5), seriestype=:shape, alpha=0.3, color=:blue, label="A")
plot!(p1, circle(0.3,0,0.5), seriestype=:shape, alpha=0.3, color=:red, label="B")
plot!(p1, xlims=(-1.5,1.5), ylims=(-1.5,1.5), aspect_ratio=:equal)

# Probabilidade condicional
p2 = plot!(subplot=2, title="P(A|B)")
plot!(p2, circle(0.3,0,0.5), seriestype=:shape, alpha=0.3, color=:red, label="B")
plot!(p2, circle(-0.3,0,0.5), seriestype=:shape, alpha=0.3, color=:blue, label="A∩B")
plot!(p2, xlims=(-1.5,1.5), ylims=(-1.5,1.5), aspect_ratio=:equal)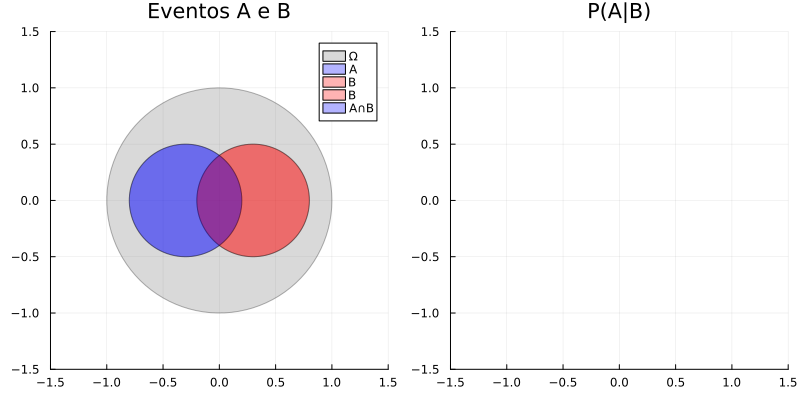

Visualização da Probabilidade Condicional

Figura 1: Interpretação geométrica da probabilidade condicional

2. Propriedades Fundamentais

2.1 Axiomas e Propriedades Básicas

Não-negatividade: $0 \leq P(A\mid B) \leq 1$
Normalização: $P(\Omega\mid B) = 1$
Aditividade: Para eventos mutuamente exclusivos $A_1$ e $A_2$: $P(A_1 \cup A_2\mid B) = P(A_1\mid B) + P(A_2\mid B)$
Complementaridade: $P(A\mid B) + P(A’\mid B) = 1$
Assimetria: $P(A\mid B) \neq P(B\mid A)$ (em geral)

2.2 Regra da Multiplicação

A regra da multiplicação estabelece que:

\[P(A \cap B) = P(B) \cdot P(A\mid B) = P(A) \cdot P(B\mid A)\]

Esta regra é fundamental para:

Calcular probabilidades de eventos compostos
Determinar independência entre eventos
Resolver problemas de probabilidade sequencial

2.3 Lei da Probabilidade Total

Para uma partição ${B_1, B_2, …, B_n}$ do espaço amostral:

\[P(A) = \sum_{i=1}^n P(A\mid B_i)P(B_i)\]

Esta lei nos permite:

Decompor probabilidades complexas
Analisar cenários mútuamente exclusivos
Calcular probabilidades marginais

3. Independência de Eventos

3.1 Definição Formal

Dois eventos $A$ e $B$ são independentes se:

\[P(A\mid B) = P(A) \text{ ou } P(B\mid A) = P(B)\]

Equivalentemente:

\[P(A \cap B) = P(A) \cdot P(B)\]

3.2 Verificação de Independência

julia

using Random

function verificar_independencia()
    # Simulação de lançamento de dois dados
    n_simulacoes = 10000
    Random.seed!(123)
    
    # Gerando lançamentos
    dado1 = rand(1:6, n_simulacoes)
    dado2 = rand(1:6, n_simulacoes)
    
    # Eventos
    A = dado1 .> 3  # Primeiro dado maior que 3
    B = dado2 .% 2 .== 0  # Segundo dado é par
    
    # Calculando probabilidades
    PA = mean(A)
    PB = mean(B)
    PAB = mean(A .& B)
    
    println("P(A) = ", round(PA, digits=4))
    println("P(B) = ", round(PB, digits=4))
    println("P(A∩B) = ", round(PAB, digits=4))
    println("P(A)⋅P(B) = ", round(PA*PB, digits=4))
end

verificar_independencia()

4. Teorema de Bayes

O Teorema de Bayes é um princípio fundamental da estatística que descreve a maneira como atualizamos nossas crenças em relação a um evento, com base em novas evidências. Ele é amplamente utilizado em probabilidade e estatística, principalmente em problemas onde precisamos revisar previsões ou hipóteses à medida que recebemos mais informações.

4.1 Formulação e Intuição

O Teorema de Bayes pode ser expresso matematicamente como:

\[P(A\mid B) = \frac{P(B\mid A)P(A)}{P(B)}\]

Onde cada termo tem um significado específico:

$P(A\mid B)$ é a probabilidade posterior: probabilidade de $A$ acontecer dado que $B$ já aconteceu
$P(B\mid A)$ é a probabilidade verossímil: probabilidade de $B$ acontecer dado que $A$ é verdadeiro
$P(A)$ é a probabilidade anterior ou priori: probabilidade de $A$ acontecer sem informação adicional
$P(B)$ é a probabilidade marginal: probabilidade de $B$ acontecer, considerando todas as hipóteses

💡 Dica:
Sempre que se tem uma condicional, o espaço amostral se restringe ao evento dado. Por isso, a probabilidade posterior $P(A\mid B)$ considera apenas o espaço onde $B$ ocorreu.

4.2 Componentes e Interpretação

Probabilidade Anterior (Prior)
- Representa nosso conhecimento inicial
- Baseada em informações prévias ou experiência
- Pode ser subjetiva ou baseada em dados históricos
Verossimilhança
- Representa a evidência observada
- Mede quão provável é observar os dados sob diferentes hipóteses
- Atualiza nossa crença inicial
Probabilidade Posterior
- Combina prior e verossimilhança
- Representa nossa crença atualizada
- Base para tomada de decisões

4.3 Exemplo Prático: Teste Diagnóstico

Considere um teste diagnóstico para uma doença $D$, onde:

$P(D) = 0,01$ (1% da população tem a doença)
$P(T^+\mid D) = 0,99$ (99% de sensibilidade do teste)
$P(T^+\mid D^c) = 0,05$ (5% de falsos positivos)

A probabilidade total de um teste positivo é:

$P(T^+) = P(T^+\mid D)P(D) + P(T^+\mid D^c)P(D^c)$ $P(T^+) = (0,99 \cdot 0,01) + (0,05 \cdot 0,99) = 0,0594$

Aplicando Bayes para encontrar a probabilidade de ter a doença dado um teste positivo:

\[P(D\mid T^+) = \frac{P(T^+\mid D)P(D)}{P(T^+)} = \frac{0,99 \cdot 0,01}{0,0594} \approx 0,1667\]

julia

function exemplo_bayes()
    # Parâmetros do problema
    P_D = 0.01    # P(D) - prevalência
    P_TD = 0.99   # P(T+|D) - sensibilidade
    P_TnD = 0.05  # P(T+|não D) - taxa falso positivo
    
    # Probabilidade marginal P(T+)
    P_T = P_TD * P_D + P_TnD * (1 - P_D)
    
    # Teorema de Bayes
    P_DT = (P_TD * P_D) / P_T
    
    println("Análise do Teste Diagnóstico:")
    println("-----------------------------")
    println("Prevalência da doença: ", round(P_D * 100, digits=1), "%")
    println("Sensibilidade do teste: ", round(P_TD * 100, digits=1), "%")
    println("Taxa de falso positivo: ", round(P_TnD * 100, digits=1), "%")
    println("-----------------------------")
    println("Probabilidade de doença dado teste positivo: ",
            round(P_DT * 100, digits=1), "%")
end

exemplo_bayes()

4.4 Aplicações em Diferentes Áreas

Medicina e Diagnóstico
- Interpretação de testes clínicos
- Avaliação de riscos em saúde
- Estudos epidemiológicos
- Medicina personalizada
Machine Learning e IA
- Classificadores Bayesianos
- Redes Bayesianas
- Sistemas de recomendação
- Processamento de linguagem natural
- Filtros de spam
Finanças e Economia
- Análise de risco
- Previsão de mercado
- Detecção de fraudes
- Avaliação de investimentos
Ciências Sociais
- Pesquisas de opinião
- Análise de comportamento
- Estudos demográficos
- Previsões eleitorais

4.5 Considerações Práticas

Escolha da Prior
- Use dados históricos quando disponíveis
- Considere opinião de especialistas
- Utilize priors não-informativas quando apropriado
Atualização Sequencial
- A posterior de uma análise pode ser prior da próxima
- Permite aprendizado incremental
- Útil em análise de dados em tempo real
Limitações
- Sensibilidade à escolha da prior
- Necessidade de probabilidades bem definidas
- Complexidade computacional em alguns casos

4.5 Teorema de Bayes com Partições

Uma partição é um conjunto de eventos mutuamente exclusivos e coletivamente exaustivos que cobrem todo o espaço amostral. Em outras palavras, cada resultado possível pertence a exatamente um desses eventos.

4.5.1 Formulação com Partições

Para uma partição formada pelos eventos $A_1, A_2, \dots, A_n$ e um evento $B$, o Teorema de Bayes é expresso como:

\[P(A_i\mid B) = \frac{P(B\mid A_i)P(A_i)}{\sum_{j=1}^{n} P(B\mid A_j)P(A_j)}\]

Onde:

Partição: $A_1, A_2, \dots, A_n$ são eventos que formam uma partição do espaço amostral
- Mutuamente exclusivos: $A_i \cap A_j = \emptyset$ para $i \neq j$
- Coletivamente exaustivos: $\bigcup_{i=1}^{n} A_i = \Omega$
Probabilidade posterior: $P(A_i\mid B)$
Probabilidade verossímil: $P(B\mid A_i)$
Probabilidade anterior: $P(A_i)$
Probabilidade marginal: $\sum_{j=1}^{n} P(B\mid A_j)P(A_j)$

4.5.2 Exemplo: Controle de Qualidade

Considere uma empresa com três fábricas que produzem o mesmo produto:

julia

function exemplo_bayes_particoes()
    # Probabilidades das fábricas (prior)
    P_A = [0.5, 0.3, 0.2]  # P(A₁), P(A₂), P(A₃)
    
    # Probabilidades de defeito por fábrica
    P_BA = [0.02, 0.03, 0.04]  # P(B|A₁), P(B|A₂), P(B|A₃)
    
    # Probabilidade total de defeito (lei das probabilidades totais)
    P_B = sum(P_BA .* P_A)
    
    # Probabilidades posteriores (Teorema de Bayes)
    P_AB = P_BA .* P_A ./ P_B
    
    println("Análise de Controle de Qualidade")
    println("--------------------------------")
    println("Probabilidade total de defeito: ", round(P_B * 100, digits=2), "%")
    println("\nProbabilidade de origem dado defeito:")
    for (i, p) in enumerate(P_AB)
        println("Fábrica ", i, ": ", round(p * 100, digits=2), "%")
    end
end

exemplo_bayes_particoes()

Dados:

Probabilidades de produção (prior):
- $P(A_1) = 0,5$ (Fábrica 1)
- $P(A_2) = 0,3$ (Fábrica 2)
- $P(A_3) = 0,2$ (Fábrica 3)
Probabilidades de defeito por fábrica:
- $P(B\mid A_1) = 0,02$ (2% de defeitos na Fábrica 1)
- $P(B\mid A_2) = 0,03$ (3% de defeitos na Fábrica 2)
- $P(B\mid A_3) = 0,04$ (4% de defeitos na Fábrica 3)

Probabilidade Total de Defeito: $P(B) = \sum_{j=1}^{3} P(B\mid A_j)P(A_j)$ $P(B) = (0,02 \cdot 0,5) + (0,03 \cdot 0,3) + (0,04 \cdot 0,2) = 0,029$
Probabilidade da Fábrica 2 dado Defeito: $P(A_2\mid B) = \frac{P(B\mid A_2)P(A_2)}{P(B)} = \frac{0,03 \cdot 0,3}{0,029} \approx 0,3103$

Portanto:

A probabilidade total de um produto ser defeituoso é 2,9%
Se um produto é defeituoso, há aproximadamente 31,03% de chance de ter sido produzido pela Fábrica 2

4.5.3 Importância das Partições

O uso de partições no Teorema de Bayes é fundamental para:

Análise Completa
- Considera todas as possibilidades mutuamente exclusivas
- Garante que nenhum caso seja omitido
- Permite análise sistemática
Tomada de Decisão
- Avalia múltiplas hipóteses simultaneamente
- Compara probabilidades entre diferentes cenários
- Facilita escolhas baseadas em evidências
Aplicações Práticas
- Diagnóstico médico com múltiplas causas
- Classificação em machine learning
- Análise de falhas em sistemas complexos
- Avaliação de riscos em projetos

5. Aplicações e Exemplos Práticos

5.1 Medicina e Diagnóstico

Testes diagnósticos
Estudos epidemiológicos
Análise de risco em saúde
Triagem de pacientes

5.2 Finanças e Economia

Análise de risco de crédito
Previsão de mercado
Decisões de investimento
Avaliação de seguros

5.3 Machine Learning e IA

Classificadores Bayesianos
Redes Bayesianas
Sistemas de recomendação
Processamento de linguagem natural

5.4 Ciências Sociais

Pesquisas de opinião
Análise de comportamento
Estudos demográficos
Previsões eleitorais

6. Exercícios Práticos

6.1 Exercício Resolvido: Estudo Epidemiológico

Ilustração de carrapatos

Figura: Diferentes tipos de carrapatos que podem transmitir doenças

Problema: Carrapatos podem transportar tanto a doença de Lyme quanto a erliquiose granulocítica humana (HGE). Em um estudo com carrapatos no mid-west americano foi descoberto que:

16% dos carrapatos eram portadores da doença de Lyme

10% eram portadores do HGE

10% dos carrapatos que eram portadores da doença de Lyme ou HGE, eram portadores de ambas doenças

Questões:

a) Qual a probabilidade $\Pr[\text{Lyme} \cap \text{HGE}]$ de que um carrapato seja portador de ambas as doenças?
b) Qual a probabilidade condicional de que um carrapato seja portador do HGE, dado que ele é portador da doença de Lyme?

Dados do problema:

$ \Pr[\text{Lyme}] = 0,16 $ (16% dos carrapatos são portadores da doença de Lyme).
$ \Pr[\text{HGE}] = 0,10 $ (10% dos carrapatos são portadores de HGE).
10% dos carrapatos que tinham Lyme ou HGE eram portadores de ambas as doenças.

Parte (a): Encontrar $ \Pr[\text{Lyme} \cap \text{HGE}] $

A probabilidade de que um carrapato seja portador de ambas as doenças é dada por:

\[0,10 \cdot \Pr[\text{Lyme} \cup \text{HGE}] = \Pr[\text{Lyme} \cap \text{HGE}]\]

Sabemos que:

\[\Pr[\text{Lyme} \cup \text{HGE}] = \Pr[\text{Lyme}] + \Pr[\text{HGE}] - \Pr[\text{Lyme} \cap \text{HGE}]\]

Substituindo esses valores:

\[0,10 \cdot (0,16 + 0,10 - \Pr[\text{Lyme} \cap \text{HGE}]) = \Pr[\text{Lyme} \cap \text{HGE}]\]

Resolvendo a equação:

\[0,10 \cdot (0,26 - \Pr[\text{Lyme} \cap \text{HGE}]) = \Pr[\text{Lyme} \cap \text{HGE}]\] \[0,026 - 0,10 \cdot \Pr[\text{Lyme} \cap \text{HGE}] = \Pr[\text{Lyme} \cap \text{HGE}]\] \[0,026 = \Pr[\text{Lyme} \cap \text{HGE}] + 0,10 \cdot \Pr[\text{Lyme} \cap \text{HGE}]\] \[0,026 = 1,10 \cdot \Pr[\text{Lyme} \cap \text{HGE}]\] \[\Pr[\text{Lyme} \cap \text{HGE}] = \frac{0,026}{1,10} = 0,0236\]

Portanto, a probabilidade de um carrapato ser portador de ambas as doenças é $ \Pr[\text{Lyme} \cap \text{HGE}] = 0,0236 $.

Parte (b): Probabilidade condicional de que um carrapato seja portador do HGE, dado que ele é portador da doença de Lyme

A probabilidade condicional de HGE dado Lyme é dada por:

\[\Pr[\text{HGE} | \text{Lyme}] = \frac{\Pr[\text{Lyme} \cap \text{HGE}]}{\Pr[\text{Lyme}]}\]

Substituindo os valores:

\[\Pr[\text{HGE} | \text{Lyme}] = \frac{0,0236}{0,16} = 0,1475\]

Portanto, a probabilidade de que um carrapato seja portador de HGE, dado que ele é portador da doença de Lyme, é $ \Pr[\text{HGE} | \text{Lyme}] \approx 0,1475 $.

julia

function resolver_problema_carrapatos()
    # Dados do problema
    Pr_Lyme = 0.16  # Pr[Lyme]
    Pr_HGE = 0.10   # Pr[HGE]
    prop_intersecao = 0.10
    
    # Cálculo iterativo
    Pr_intersecao = 0.0
    tolerancia = 1e-6
    
    for _ in 1:1000
        # Pr[Lyme ∪ HGE] usando a interseção atual
        Pr_uniao = Pr_Lyme + Pr_HGE - Pr_intersecao
        
        # Nova Pr[Lyme ∩ HGE]
        Pr_intersecao_novo = prop_intersecao * Pr_uniao
        
        # Verificar convergência
        if abs(Pr_intersecao_novo - Pr_intersecao) < tolerancia
            break
        end
        
        Pr_intersecao = Pr_intersecao_novo
    end
    
    # Probabilidade condicional
    Pr_HGE_dado_Lyme = Pr_intersecao / Pr_Lyme
    
    println("Análise Epidemiológica - Carrapatos")
    println("-----------------------------------")
    println("Pr[Lyme ∩ HGE] = ", round(Pr_intersecao, digits=4))
    println("Pr[HGE|Lyme] = ", round(Pr_HGE_dado_Lyme, digits=4))
end

resolver_problema_carrapatos()

6.2 Exercício Resolvido: Teste de HIV

Problema: Suponha que para a população em geral, 1 em cada 5000 pessoas carrega o vírus HIV e que existe um teste para a presença do HIV cujo os possíveis resultados são positivo (+) e negativo (−). Suponha que o teste acerte a resposta em 99% dos casos, isto é, para uma pessoa que tem HIV ou não, o teste dá o resultado correto 99% das vezes.

Questões:

a) Qual é a probabilidade $\Pr[-\mid\text{HIV}]$ de que o teste dê negativo dado que a pessoa possui o vírus HIV?
b) Qual a probabilidade $\Pr[\text{HIV}\mid +]$ de que uma pessoa escolhida aleatoriamente tenha o vírus HIV dado que o teste deu positivo?

Dados do problema:

Prevalência do HIV: $\Pr[\text{HIV}] = \frac{1}{5000} = 0,0002$ (0,02% da população tem HIV)
Probabilidade de testar positivo se a pessoa tem HIV (verdadeiro positivo): $\Pr[+\mid\text{HIV}] = 0,99$
Probabilidade de testar negativo se a pessoa não tem HIV (verdadeiro negativo): $\Pr[-\mid\neg\text{HIV}] = 0,99$

Parte (a): Probabilidade de testar negativo dado que a pessoa tem HIV

A probabilidade de um teste dar negativo dado que a pessoa tem HIV é a complementação da probabilidade de um teste dar positivo para quem tem HIV:

\[\Pr[-\mid\text{HIV}] = 1 - \Pr[+\mid\text{HIV}] = 1 - 0,99 = 0,01\]

Portanto, a probabilidade de que o teste dê negativo dado que a pessoa possui o vírus HIV é $\Pr[-\mid\text{HIV}] = 0,01$ ou 1%.

Parte (b): Probabilidade de ter HIV dado que o teste deu positivo

Para calcular essa probabilidade, usaremos o Teorema de Bayes:

\[\Pr[\text{HIV}\mid +] = \frac{\Pr[+\mid\text{HIV}] \cdot \Pr[\text{HIV}]}{\Pr[+]}\]

Onde $\Pr[+]$ (probabilidade total de testar positivo) pode ser calculada considerando dois casos:

A pessoa tem HIV e o teste acerta (positivo)
A pessoa não tem HIV e o teste erra (falso positivo)

Cálculo de $\Pr[+]$:

\[\Pr[+] = \Pr[+\mid\text{HIV}] \cdot \Pr[\text{HIV}] + \Pr[+\mid\neg\text{HIV}] \cdot \Pr[\neg\text{HIV}]\]

Sabemos que:

$\Pr[\neg\text{HIV}] = 1 - \Pr[\text{HIV}] = 1 - 0,0002 = 0,9998$
A probabilidade de testar positivo para quem não tem HIV (falso positivo) é

\[\Pr[+\mid\neg\text{HIV}] = 1 - \Pr[-\mid\neg\text{HIV}] = 1 - 0,99 = 0,01\]

Substituindo os valores:

\[\Pr[+] = (0,99 \cdot 0,0002) + (0,01 \cdot 0,9998) = 0,000198 + 0,009998 = 0,010196\]

Agora, podemos aplicar o Teorema de Bayes:

\[\Pr[\text{HIV}\mid +] = \frac{\Pr[+\mid\text{HIV}] \cdot \Pr[\text{HIV}]}{\Pr[+]} = \frac{0,99 \cdot 0,0002}{0,010196} \approx 0,0194\]

Portanto, a probabilidade de que uma pessoa escolhida aleatoriamente tenha o vírus HIV dado que o teste deu positivo é aproximadamente $\Pr[\text{HIV}\mid +] \approx 0,0194$ ou 1,94%.

julia

function resolver_problema_hiv()
    # Dados do problema
    Pr_HIV = 1/5000  # Prevalência do HIV
    Pr_pos_dado_HIV = 0.99  # Sensibilidade
    Pr_neg_dado_naoHIV = 0.99  # Especificidade
    
    # Parte (a)
    Pr_neg_dado_HIV = 1 - Pr_pos_dado_HIV
    
    # Parte (b)
    Pr_naoHIV = 1 - Pr_HIV
    Pr_pos_dado_naoHIV = 1 - Pr_neg_dado_naoHIV
    
    # Probabilidade total de teste positivo
    Pr_pos = (Pr_pos_dado_HIV * Pr_HIV) + (Pr_pos_dado_naoHIV * Pr_naoHIV)
    
    # Teorema de Bayes
    Pr_HIV_dado_pos = (Pr_pos_dado_HIV * Pr_HIV) / Pr_pos
    
    println("Análise do Teste de HIV")
    println("----------------------")
    println("Pr[-|HIV] = ", round(Pr_neg_dado_HIV, digits=4))
    println("Pr[HIV|+] = ", round(Pr_HIV_dado_pos, digits=4))
end

resolver_problema_hiv()

Parte (c): Cenário Inverso - Probabilidade de não ter HIV dado que o teste deu negativo

Este cenário complementar é importante para entender a confiabilidade do teste quando o resultado é negativo. Usaremos novamente o Teorema de Bayes:

\[\Pr[\neg\text{HIV}\mid -] = \frac{\Pr[-\mid\neg\text{HIV}] \cdot \Pr[\neg\text{HIV}]}{\Pr[-]}\]

Onde $\Pr[-]$ (probabilidade total de testar negativo) pode ser calculada considerando dois casos:

A pessoa não tem HIV e o teste acerta (verdadeiro negativo)
A pessoa tem HIV e o teste erra (falso negativo)

Cálculo de $\Pr[-]$:

\[\Pr[-] = \Pr[-\mid\neg\text{HIV}] \cdot \Pr[\neg\text{HIV}] + \Pr[-\mid\text{HIV}] \cdot \Pr[\text{HIV}]\]

Substituindo os valores:

$\Pr[-\mid\neg\text{HIV}] = 0,99$ (verdadeiro negativo)
$\Pr[\neg\text{HIV}] = 0,9998$
$\Pr[-\mid\text{HIV}] = 0,01$ (falso negativo)
$\Pr[\text{HIV}] = 0,0002$

\[\Pr[-] = (0,99 \cdot 0,9998) + (0,01 \cdot 0,0002) = 0,989802 + 0,000002 = 0,989804\]

Agora, podemos aplicar o Teorema de Bayes:

\[\Pr[\neg\text{HIV}\mid -] = \frac{0,99 \cdot 0,9998}{0,989804} \approx 0,99999798\]

Portanto, a probabilidade de que uma pessoa não tenha HIV dado que o teste deu negativo é aproximadamente $\Pr[\neg\text{HIV}\mid -] \approx 0,99999798$ ou 99,999798%.

Este resultado mostra que o teste é extremamente confiável quando dá negativo, com uma probabilidade muito próxima de 100% de a pessoa realmente não ter HIV nesse caso.

Resumo dos Resultados:

Probabilidade de falso negativo:

\[\Pr[-\mid\text{HIV}] = 0,01\]

Probabilidade de ter HIV dado positivo:

\[\Pr[\text{HIV}\mid +] \approx 0,0194\]

Probabilidade de não ter HIV dado negativo:

\[\Pr[\neg\text{HIV}\mid -] \approx 0,99999798\]

julia

function analise_completa_hiv()
    # Dados do problema
    Pr_HIV = 1/5000  # Prevalência do HIV
    Pr_pos_dado_HIV = 0.99  # Sensibilidade
    Pr_neg_dado_naoHIV = 0.99  # Especificidade
    
    # Cálculos auxiliares
    Pr_naoHIV = 1 - Pr_HIV
    Pr_neg_dado_HIV = 1 - Pr_pos_dado_HIV
    Pr_pos_dado_naoHIV = 1 - Pr_neg_dado_naoHIV
    
    # Probabilidade total de teste positivo
    Pr_pos = (Pr_pos_dado_HIV * Pr_HIV) + (Pr_pos_dado_naoHIV * Pr_naoHIV)
    
    # Probabilidade total de teste negativo
    Pr_neg = (Pr_neg_dado_naoHIV * Pr_naoHIV) + (Pr_neg_dado_HIV * Pr_HIV)
    
    # Teorema de Bayes - Cenários
    Pr_HIV_dado_pos = (Pr_pos_dado_HIV * Pr_HIV) / Pr_pos
    Pr_naoHIV_dado_neg = (Pr_neg_dado_naoHIV * Pr_naoHIV) / Pr_neg
    
    println("Análise Completa do Teste de HIV")
    println("-------------------------------")
    println("Falso negativo Pr[-|HIV] = ", round(Pr_neg_dado_HIV, digits=4))
    println("HIV dado positivo Pr[HIV|+] = ", round(Pr_HIV_dado_pos, digits=8))
    println("Não HIV dado negativo Pr[¬HIV|-] = ", round(Pr_naoHIV_dado_neg, digits=8))
end

analise_completa_hiv()

6.3 Exercício Resolvido: Controle de Qualidade

Ilustração de controle de qualidade

Figura: Processo de controle de qualidade em linha de produção

Problema: Suponha que em uma fábrica, 2 em cada 1000 produtos são defeituosos. A fábrica realiza um teste de qualidade que pode resultar em defeituoso (D) ou em perfeitas condições (E). Suponha que o teste acerte a resposta em 95% dos casos, isto é, para um produto que é defeituoso ou não, o teste dá o resultado correto 95% das vezes.

Questões:

a) Qual é a probabilidade $\Pr[T_d\mid E]$ de que o teste dê resultado defeituoso dado que o produto está em perfeitas condições?
b) Qual a probabilidade $\Pr[D\mid T_d]$ de que um produto escolhido aleatoriamente seja defeituoso dado que o teste deu resultado defeituoso?

Dados do problema:

Probabilidade de um produto ser defeituoso:

$\Pr[D] = \frac{2}{1000} = 0,002$ (0,2%)

Probabilidade de um produto estar em perfeitas condições:

$\Pr[E] = 1 - \Pr[D] = 0,998$ (99,8%)

Acurácia do teste: 95%
- Se o produto é defeituoso, probabilidade de teste indicar defeituoso: $\Pr[T_d\mid D] = 0,95$
- Se o produto é perfeito, probabilidade de teste indicar perfeito: $\Pr[T_e\mid E] = 0,95$

Portanto:

Probabilidade de falso positivo (teste indicar defeituoso para produto perfeito): $\Pr[T_d\mid E] = 1 - \Pr[T_e\mid E] = 0,05$
Probabilidade de falso negativo (teste indicar perfeito para produto defeituoso): $\Pr[T_e\mid D] = 1 - \Pr[T_d\mid D] = 0,05$

Parte (a): Probabilidade de falso positivo

A probabilidade de que o teste dê resultado defeituoso dado que o produto está em perfeitas condições é exatamente a taxa de falso positivo:

\[\Pr[T_d\mid E] = 1 - \Pr[T_e\mid E] = 1 - 0,95 = 0,05\]

Portanto, a probabilidade de que o teste indique defeituoso para um produto em perfeitas condições é $\Pr[T_d\mid E] = 0,05$ ou 5%.

Parte (b): Probabilidade de defeito dado teste positivo

Para calcular a probabilidade de um produto ser realmente defeituoso dado que o teste indicou defeito, usamos o Teorema de Bayes:

\[\Pr[D\mid T_d] = \frac{\Pr[T_d\mid D] \cdot \Pr[D]}{\Pr[T_d]}\]

Onde $\Pr[T_d]$ (probabilidade total de teste indicar defeito) pode ser calculada considerando dois casos:

O produto é defeituoso e o teste acerta (verdadeiro positivo)
O produto é perfeito e o teste erra (falso positivo)

Cálculo de $\Pr[T_d]$:

\[\Pr[T_d] = \Pr[T_d\mid D] \cdot \Pr[D] + \Pr[T_d\mid E] \cdot \Pr[E]\]

Substituindo os valores:

\[\Pr[T_d] = (0,95 \cdot 0,002) + (0,05 \cdot 0,998) = 0,0019 + 0,0499 = 0,0518\]

Agora, podemos aplicar o Teorema de Bayes:

\[\Pr[D\mid T_d] = \frac{0,95 \cdot 0,002}{0,0518}\] \[\Pr[D\mid T_d] = \frac{0,0019}{0,0518} \approx 0,0367\]

Portanto, a probabilidade de que um produto seja realmente defeituoso dado que o teste indicou defeito é aproximadamente $\Pr[D\mid T_d] \approx 0,0367$ ou 3,67%.

Interpretação dos Resultados

A probabilidade de falso positivo (5%) é relativamente alta, o que significa que o teste frequentemente indica defeitos em produtos bons.
Quando o teste indica defeito, há apenas 3,67% de chance de o produto ser realmente defeituoso.
Este baixo valor positivo preditivo ocorre porque:
- A prevalência de defeitos é muito baixa (0,2%)
- A taxa de falsos positivos (5%) é alta em comparação com a prevalência

julia

function analise_controle_qualidade()
    # Dados do problema
    Pr_D = 2/1000  # Probabilidade de defeito
    Pr_E = 1 - Pr_D  # Probabilidade de perfeito
    
    # Características do teste
    Pr_Td_D = 0.95  # Sensibilidade
    Pr_Te_E = 0.95  # Especificidade
    
    # Probabilidades complementares
    Pr_Td_E = 1 - Pr_Te_E  # Falso positivo
    
    # Probabilidade total de teste indicar defeito
    Pr_Td = (Pr_Td_D * Pr_D) + (Pr_Td_E * Pr_E)
    
    # Teorema de Bayes
    Pr_D_Td = (Pr_Td_D * Pr_D) / Pr_Td
    
    println("Análise de Controle de Qualidade")
    println("-------------------------------")
    println("Falso positivo Pr[Td|E] = ", round(Pr_Td_E, digits=4))
    println("Defeito dado teste positivo Pr[D|Td] = ", round(Pr_D_Td, digits=4))
end

analise_controle_qualidade()

6.4 Exercício Resolvido: Previsão do Tempo

Ilustração de previsão do tempo

Figura: Previsão meteorológica e probabilidade de chuva

Problema: Suponha que, em uma determinada cidade, 1 em cada 10 dias de verão apresenta chuvas. Um meteorologista utiliza um modelo de previsão do tempo que, em média, acerta a previsão de chuvas em 80% dos casos. Isso significa que, se vai chover, o modelo tem 80% de chance de prever “chuva”, e se não vai chover, ele tem 80% de chance de prever “sem chuva”.

Questões:

a) Qual é a probabilidade $P(S\mid C)$ de que o modelo preveja “sem chuva” dado que realmente vai chover?
b) Qual a probabilidade $P(C\mid S)$ de que realmente vai chover dado que o modelo previu “sem chuva”?

Dados do problema:

A probabilidade de chover em um dia de verão é:

\[P(C) = \frac{1}{10} = 0,1\]

A probabilidade de não chover em um dia de verão é:

\[P(NC) = 1 - P(C) = 0,9\]

O modelo de previsão acerta 80% dos casos:
- Se vai chover, a probabilidade de o modelo prever “chuva” é:
\[P(P_C \mid C) = 0,8\]
- Se não vai chover, a probabilidade de o modelo prever “sem chuva” é:
\[P(P_{NC} \mid NC) = 0,8\]

Portanto:

A probabilidade de o modelo prever “sem chuva” quando realmente vai chover é: $P(P_{NC} \mid C) = 1 - P(P_C \mid C) = 0,2$
A probabilidade de o modelo prever “chuva” quando realmente não vai chover é: $P(P_C \mid NC) = 1 - P(P_{NC} \mid NC) = 0,2$

Parte (a): Probabilidade de previsão “sem chuva” dado que vai chover

A probabilidade já é conhecida: $P(S \mid C) = P(P_{NC} \mid C) = 0,2$

Portanto, a probabilidade de que o modelo preveja “sem chuva” dado que realmente vai chover é $P(S \mid C) = 0,2$ ou 20%.

Parte (b): Probabilidade de chover dado previsão “sem chuva”

Para calcular a probabilidade de que realmente vai chover dado que o modelo previu “sem chuva”, usamos o Teorema de Bayes:

\[P(C \mid S) = \frac{P(S \mid C) \cdot P(C)}{P(S)}\]

Onde $P(S)$ (probabilidade total de previsão “sem chuva”) pode ser calculada considerando dois casos:

Vai chover e o modelo erra (falso negativo)
Não vai chover e o modelo acerta (verdadeiro negativo)

Cálculo de $P(S)$:

\[P(S) = P(S \mid C) \cdot P(C) + P(S \mid NC) \cdot P(NC)\]

Substituindo os valores:

\[P(S) = (0,2 \cdot 0,1) + (0,8 \cdot 0,9) = 0,02 + 0,72 = 0,74\]

Agora, podemos aplicar o Teorema de Bayes:

\[P(C \mid S) = \frac{0,2 \cdot 0,1}{0,74} = \frac{0,02}{0,74} \approx 0,027\]

Portanto, a probabilidade de que realmente vai chover dado que o modelo previu “sem chuva” é aproximadamente $P(C \mid S) \approx 0,027$ ou 2,7%.

julia

function analise_previsao_tempo()
    # Dados do problema
    P_C = 1/10  # Probabilidade de chuva
    P_NC = 1 - P_C  # Probabilidade de não chuva
    
    # Características do modelo
    P_PC_C = 0.8  # Sensibilidade (acerto quando chove)
    P_PNC_NC = 0.8  # Especificidade (acerto quando não chove)
    
    # Probabilidades complementares
    P_PNC_C = 1 - P_PC_C  # Falso negativo
    
    # Probabilidade total de previsão "sem chuva"
    P_S = (P_PNC_C * P_C) + (P_PNC_NC * P_NC)
    
    # Teorema de Bayes
    P_C_S = (P_PNC_C * P_C) / P_S
    
    println("Análise da Previsão do Tempo")
    println("---------------------------")
    println("P(S|C) = ", round(P_PNC_C, digits=4))
    println("P(C|S) = ", round(P_C_S, digits=4))
end

analise_previsao_tempo()

6.5 Teste Diagnóstico

Calcule a probabilidade de um paciente ter uma doença dado um teste positivo
- Considere diferentes valores de sensibilidade e especificidade
- Analise como a prevalência afeta o resultado
Calcule a probabilidade de tirar um ás dado que a carta é vermelha
- Compare com a probabilidade de tirar uma carta vermelha dado que é um ás
- Verifique a independência entre naipe e valor
Verifique a independência entre diferentes eventos
- Calcule probabilidades condicionais para somas e produtos
- Analise sequências de lançamentos

7. Considerações Práticas

7.1 Limitações e Cuidados

Necessidade de dados suficientes
Independência das observações
Viés de seleção
Causalidade vs. correlação

7.2 Boas Práticas

Validação de pressupostos
Análise de sensibilidade
Documentação clara
Interpretação cuidadosa

Referências

Ross, S. M. A First Course in Probability. 9ª ed. Pearson, 2012.
Feller, W. An Introduction to Probability Theory and Its Applications. Vol. 1, 3ª ed. Wiley, 1968.
DeGroot, M. H.; Schervish, M. J. Probability and Statistics. 4ª ed. Pearson, 2011.
Morettin, P. A.; Bussab, W. O. Estatística Básica. 9ª ed. Saraiva, 2017.
Magalhães, M. N. Probabilidade e Variáveis Aleatórias. 3ª ed. EDUSP, 2015.
James, B. R. Probabilidade: Um Curso em Nível Intermediário. 3ª ed. IMPA, 2004.

Morrison Külsenn

Estatística Pura

Probabilidade Condicional

1. Definição e Conceitos Básicos

1.1 Definição Formal

1.2 Interpretação Geométrica

2. Propriedades Fundamentais

2.1 Axiomas e Propriedades Básicas

2.2 Regra da Multiplicação

2.3 Lei da Probabilidade Total

3. Independência de Eventos

3.1 Definição Formal

3.2 Verificação de Independência

4. Teorema de Bayes

4.1 Formulação e Intuição

4.2 Componentes e Interpretação

4.3 Exemplo Prático: Teste Diagnóstico

4.4 Aplicações em Diferentes Áreas

4.5 Considerações Práticas

4.5 Teorema de Bayes com Partições

4.5.1 Formulação com Partições

4.5.2 Exemplo: Controle de Qualidade

4.5.3 Importância das Partições

5. Aplicações e Exemplos Práticos

5.1 Medicina e Diagnóstico

5.2 Finanças e Economia

5.3 Machine Learning e IA

5.4 Ciências Sociais

6. Exercícios Práticos

6.1 Exercício Resolvido: Estudo Epidemiológico

Dados do problema:

Parte (a): Encontrar $ \Pr[\text{Lyme} \cap \text{HGE}] $

Portanto, a probabilidade de um carrapato ser portador de ambas as doenças é $ \Pr[\text{Lyme} \cap \text{HGE}] = 0,0236 $.

Parte (b): Probabilidade condicional de que um carrapato seja portador do HGE, dado que ele é portador da doença de Lyme

Portanto, a probabilidade de que um carrapato seja portador de HGE, dado que ele é portador da doença de Lyme, é $ \Pr[\text{HGE} | \text{Lyme}] \approx 0,1475 $.

6.2 Exercício Resolvido: Teste de HIV

Dados do problema:

Parte (a): Probabilidade de testar negativo dado que a pessoa tem HIV

Portanto, a probabilidade de que o teste dê negativo dado que a pessoa possui o vírus HIV é $\Pr[-\mid\text{HIV}] = 0,01$ ou 1%.

Parte (b): Probabilidade de ter HIV dado que o teste deu positivo

Portanto, a probabilidade de que uma pessoa escolhida aleatoriamente tenha o vírus HIV dado que o teste deu positivo é aproximadamente $\Pr[\text{HIV}\mid +] \approx 0,0194$ ou 1,94%.

Parte (c): Cenário Inverso - Probabilidade de não ter HIV dado que o teste deu negativo

Portanto, a probabilidade de que uma pessoa não tenha HIV dado que o teste deu negativo é aproximadamente $\Pr[\neg\text{HIV}\mid -] \approx 0,99999798$ ou 99,999798%.

Resumo dos Resultados:

6.3 Exercício Resolvido: Controle de Qualidade

Dados do problema:

Parte (a): Probabilidade de falso positivo

Portanto, a probabilidade de que o teste indique defeituoso para um produto em perfeitas condições é $\Pr[T_d\mid E] = 0,05$ ou 5%.

Parte (b): Probabilidade de defeito dado teste positivo

Portanto, a probabilidade de que um produto seja realmente defeituoso dado que o teste indicou defeito é aproximadamente $\Pr[D\mid T_d] \approx 0,0367$ ou 3,67%.

Interpretação dos Resultados

6.4 Exercício Resolvido: Previsão do Tempo

Dados do problema:

Parte (a): Probabilidade de previsão “sem chuva” dado que vai chover

Portanto, a probabilidade de que o modelo preveja “sem chuva” dado que realmente vai chover é $P(S \mid C) = 0,2$ ou 20%.

Parte (b): Probabilidade de chover dado previsão “sem chuva”

Portanto, a probabilidade de que realmente vai chover dado que o modelo previu “sem chuva” é aproximadamente $P(C \mid S) \approx 0,027$ ou 2,7%.

6.5 Teste Diagnóstico

7. Considerações Práticas

7.1 Limitações e Cuidados

7.2 Boas Práticas

Referências

Morrison Külsenn

Estatística Pura