Introdução
Um intervalo de confiança é uma estimativa de um parâmetro populacional baseada em uma amostra, fornecendo um intervalo de valores prováveis com um determinado nível de confiança. Em vez de estimar o parâmetro por um único valor (estimativa pontual), o intervalo de confiança fornece um intervalo de valores plausíveis.

Exemplo Prático Detalhado: Intervalo de Confiança para a Média de Resistência de Tintas
Enunciado
Uma empresa de tintas deseja garantir que a resistência de sua tinta, medida em horas até o desbotamento sob luz solar intensa, atenda ao padrão mínimo de qualidade. Para isso, foram testadas 12 amostras, resultando nos seguintes tempos (em horas):
[120, 130, 125, 128, 122, 127, 126, 124, 129, 123, 128, 125]
Calcule um intervalo de confiança de 95% para a média do tempo de resistência da tinta.
1. Fórmula do Intervalo de Confiança para a Média (σ desconhecido)
Quando o desvio padrão populacional é desconhecido, usamos a distribuição t de Student:
\[IC = \bar{x} \pm t_{\alpha/2, n-1} \cdot \frac{s}{\sqrt{n}}\]Onde:
- $\bar{x}$ = média amostral
- $t_{\alpha/2, n-1}$ = valor crítico da t de Student com $n-1$ graus de liberdade
- $s$ = desvio padrão amostral
- $n$ = tamanho da amostra
Avisos Importantes
- O intervalo de confiança não garante que a média populacional está dentro do intervalo calculado para esta amostra específica. Ele indica que, se repetíssemos o experimento muitas vezes, cerca de 95% dos intervalos calculados conteriam a verdadeira média populacional.
- A distribuição t é usada porque o desvio padrão populacional é desconhecido e o tamanho da amostra é pequeno ($n < 30$).
- Os dados devem ser aproximadamente simétricos (sem outliers extremos) para a validade do método.
2. Resolução Manual Passo a Passo
Dados:
- $n = 12$
- Dados: $[120, 130, 125, 128, 122, 127, 126, 124, 129, 123, 128, 125]$
a) Média amostral ($\bar{x}$):
\[\bar{x} = \frac{120 + 130 + 125 + 128 + 122 + 127 + 126 + 124 + 129 + 123 + 128 + 125}{12} = \frac{1507}{12} = 125,5833\]b) Desvio padrão amostral ($s$):
Calculando cada termo $(x_i - \bar{x})^2$:
- $(120 - 125,5833)^2 = 31,195$
- $(130 - 125,5833)^2 = 19,493$
- $(125 - 125,5833)^2 = 0,340$
- $(128 - 125,5833)^2 = 5,844$
- $(122 - 125,5833)^2 = 12,841$
- $(127 - 125,5833)^2 = 2,008$
- $(126 - 125,5833)^2 = 0,173$
- $(124 - 125,5833)^2 = 2,507$
- $(129 - 125,5833)^2 = 11,687$
- $(123 - 125,5833)^2 = 6,673$
- $(128 - 125,5833)^2 = 5,844$
- $(125 - 125,5833)^2 = 0,340$
Somando: \(\sum (x_i - \bar{x})^2 = 98,945\)
\[s = \sqrt{\frac{98,945}{11}} = \sqrt{8,9941} = 2,999\]c) Valor crítico t
Graus de liberdade: $n-1 = 11$
Para 95% de confiança: $t_{0,025, 11} = 2,200985$ (valor exato)
d) Erro padrão da média (SE):
\[SE = \frac{2,999}{\sqrt{12}} = \frac{2,999}{3,4641} = 0,8657\]e) Margem de erro (ME):
\[ME = 2,200985 \times 0,8657 = 1,904\]f) Intervalo de confiança
\[IC = 125,5833 \pm 1,904\] \[IC = [123,68,\ 127,49]\]Interpretação: Com 95% de confiança, a média do tempo de resistência da tinta está entre 123,68 e 127,49 horas.
3. Exemplo em Julia
using Statistics, Distributions, Plots
theme(:bright)
dados = [120, 130, 125, 128, 122, 127, 126, 124, 129, 123, 128, 125]
n = length(dados)
x̄ = mean(dados)
s = std(dados, corrected=true)
α = 0.05
t = quantile(TDist(n-1), 1 - α/2)
SE = s / sqrt(n)
ME = t * SE
IC_lower = x̄ - ME
IC_upper = x̄ + ME
println("IC 95%: [", round(IC_lower, digits=2), ", ", round(IC_upper, digits=2), "]")
# Plot melhorado
plot(1:n, dados, seriestype=:scatter, label="Dados", color=:steelblue,
xlabel="Amostra", ylabel="Resistência (horas)",
title="Intervalo de Confiança 95% para Resistência da Tinta",
legend=:bottomright, markersize=6)
# Média e intervalo de confiança
hline!([x̄], label="Média ($(round(x̄, digits=2)))", color=:darkred, linestyle=:solid, linewidth=2)
# Área do intervalo de confiança (preenchimento)
plot!([1, n], [x̄, x̄], fillrange=[IC_upper, IC_upper],
fillalpha=0.1, color=:grey, label="", linewidth=0)
plot!([1, n], [x̄, x̄], fillrange=[IC_lower, IC_lower],
fillalpha=0.1, color=:grey, label="IC 95%", linewidth=0)
# Linhas dos limites do IC
hline!([IC_lower, IC_upper], label="", color=:grey, linestyle=:dash, linewidth=1.5)
# Margem de erro (setas + anotação)
annotate!(n/2, x̄, text("ME: ±$(round(ME, digits=2))", 9, :center, :black))
plot!([n/2, n/2], [x̄, IC_upper], arrow=true, color=:grey, label="", linewidth=1.5)
plot!([n/2, n/2], [x̄, IC_lower], arrow=true, color=:grey, label="", linewidth=1.5)
# Anotações extras
annotate!(n/2, IC_upper + 0.5, text("Limite Superior: $(round(IC_upper, digits=2))", 8, :center))
annotate!(n/2, IC_lower - 0.5, text("Limite Inferior: $(round(IC_lower, digits=2))", 8, :center))
# Melhorias visuais
plot!(grid=true, minorgrid=true, size=(800, 500), ylims=(minimum(dados)-1, maximum(dados)+1))
Saída esperada:
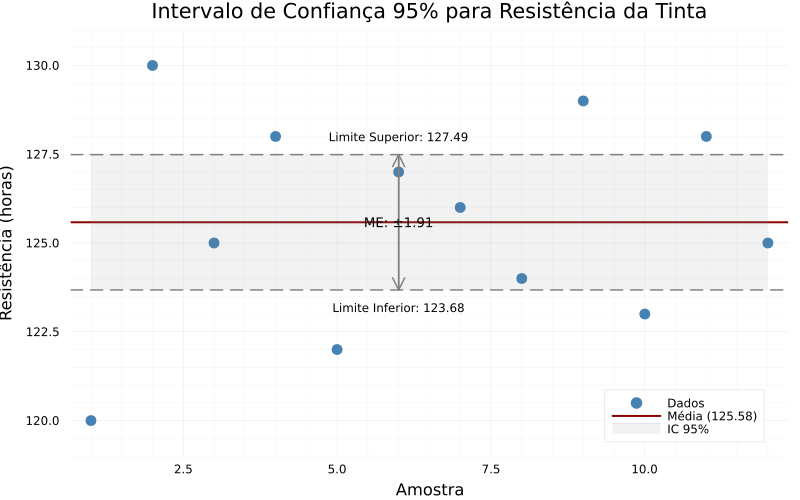
O gráfico mostra os valores individuais, a média amostral (linha vermelha tracejada) e os limites inferior e superior do intervalo de confiança (linhas verdes pontilhadas).
Contribuição Histórica de Jerzy Neyman
Jerzy Neyman (1894-1981) foi um matemático e estatístico polonês que revolucionou a teoria da inferência estatística com sua formulação dos intervalos de confiança em 1934. Sua contribuição representa um marco fundamental na transição da estatística clássica para a moderna teoria estatística.

Principais Contribuições
-
Fundamentação Teórica: Neyman desenvolveu a teoria matemática rigorosa dos intervalos de confiança, estabelecendo uma base sólida para a inferência estatística frequentista.
-
Interpretação Frequentista: Introduziu a interpretação frequentista dos intervalos de confiança, explicando que o nível de confiança se refere à frequência com que o intervalo contém o verdadeiro parâmetro em repetições hipotéticas do experimento.
-
Metodologia Objetiva: Criou uma abordagem objetiva para quantificar a incerteza em estimativas estatísticas, substituindo métodos mais subjetivos anteriores.
Legado
A formulação de Neyman dos intervalos de confiança continua sendo fundamental para:
- Pesquisa científica moderna
- Controle de qualidade industrial
- Tomada de decisões baseada em dados
- Desenvolvimento de novos métodos estatísticos
Sua abordagem rigorosa e matemática estabeleceu os fundamentos para muito do que hoje consideramos estatística moderna, incluindo a teoria da estimação e testes de hipóteses.
Conceitos Fundamentais
Nível de Confiança
O nível de confiança (geralmente representado por \(1-\alpha\)) indica a probabilidade de que o intervalo calculado contenha o verdadeiro parâmetro populacional. Os níveis mais comuns são:
- 90% (\(\alpha = 0,10\))
- 95% (\(\alpha = 0,05\))
- 99% (\(\alpha = 0,01\))
Margem de Erro
A margem de erro (ME) representa a distância máxima entre a estimativa amostral e o parâmetro populacional:
\[ME = \text{valor crítico} \times \text{erro padrão}\]Fórmula Geral
Para uma distribuição aproximadamente normal, o intervalo de confiança tem a forma geral:
\[IC = \text{Estimativa} \pm (\text{Valor crítico} \times \text{Erro padrão})\]Tipos de Intervalos de Confiança
1. Intervalo de Confiança para a Média (σ conhecido)
Quando o desvio padrão populacional (\(\sigma\)) é conhecido:
\[IC = \bar{x} \pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\]Onde:
- \(\bar{x}\) = média amostral
- \(z_{\alpha/2}\) = valor crítico da distribuição normal
- \(\sigma\) = desvio padrão populacional
- \(n\) = tamanho da amostra
Exemplo em Julia:
using Statistics, Distributions
# Dados
x̄ = 170 # média amostral
σ = 5 # desvio padrão populacional
n = 100 # tamanho da amostra
α = 0.05 # nível de significância
# Valor crítico z_(α/2)
z = quantile(Normal(), 1 - α/2)
# Erro padrão
SE = σ / sqrt(n)
# Margem de erro
ME = z * SE
# Intervalo de confiança
IC_lower = x̄ - ME
IC_upper = x̄ + ME
println("IC 95%: [$IC_lower, $IC_upper]")2. Intervalo de Confiança para a Média (σ desconhecido)
Quando o desvio padrão populacional é desconhecido:
\[IC = \bar{x} \pm t_{\alpha/2, n-1} \frac{s}{\sqrt{n}}\]Onde:
- \(s\) = desvio padrão amostral
- \(t_{\alpha/2, n-1}\) = valor crítico da distribuição t de Student
- \(n-1\) = graus de liberdade
Exemplo em Julia:
using Statistics, Distributions
# Dados amostrais
dados = [172, 168, 170, 171, 169, 167, 173, 170, 171, 168]
n = length(dados)
x̄ = mean(dados)
s = std(dados, corrected=true) # desvio padrão amostral
α = 0.05
# Valor crítico t_(α/2)
t = quantile(TDist(n-1), 1 - α/2)
# Erro padrão
SE = s / sqrt(n)
# Intervalo de confiança
IC_lower = x̄ - t * SE
IC_upper = x̄ + t * SE
println("IC 95%: [$IC_lower, $IC_upper]")3. Intervalo de Confiança para Proporção
Para uma proporção populacional:
\[IC = \hat{p} \pm z_{\alpha/2} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\]Onde:
- \(\hat{p}\) = proporção amostral
- \(n\) = tamanho da amostra
Exemplo em Julia:
using Statistics, Distributions
# Dados
sucessos = 45 # número de sucessos
n = 100 # tamanho da amostra
α = 0.05 # nível de significância
# Proporção amostral
p̂ = sucessos / n
# Valor crítico
z = quantile(Normal(), 1 - α/2)
# Erro padrão
SE = sqrt((p̂ * (1 - p̂)) / n)
# Intervalo de confiança
IC_lower = p̂ - z * SE
IC_upper = p̂ + z * SE
println("IC 95%: [$IC_lower, $IC_upper]")Interpretação Matemática
A interpretação formal do intervalo de confiança de \((1-\alpha)100\%\) é:
\[P(\text{IC contém } \mu) = 1-\alpha\]Ou mais especificamente para a média:
\[P(\bar{x} - ME \leq \mu \leq \bar{x} + ME) = 1-\alpha\]Tamanho da Amostra Necessário
Para determinar o tamanho da amostra necessário para um determinado erro máximo \(E\):
Para média (\(\sigma\) conhecido): \(n = \left(\frac{z_{\alpha/2}\sigma}{E}\right)^2\)
Para proporção: \(n = \frac{z_{\alpha/2}^2\hat{p}(1-\hat{p})}{E^2}\)
Exemplo em Julia para Cálculo do Tamanho da Amostra:
using Statistics, Distributions
# Parâmetros
E = 0.05 # erro máximo desejado
α = 0.05 # nível de significância
p̂ = 0.5 # proporção estimada (mais conservador)
z = quantile(Normal(), 1 - α/2)
# Cálculo do tamanho da amostra para proporção
n = ceil(Int, (z^2 * p̂ * (1-p̂)) / E^2)
println("Tamanho mínimo da amostra necessário: $n")Fatores que Afetam a Amplitude do Intervalo
- Nível de confiança: \(\uparrow\) confiança \(\rightarrow \uparrow\) amplitude
- Tamanho da amostra: \(\uparrow n \rightarrow \downarrow\) amplitude
- Variabilidade dos dados: \(\uparrow \sigma \text{ ou } s \rightarrow \uparrow\) amplitude
Aplicações
Os intervalos de confiança são amplamente utilizados em:
- Pesquisas de opinião
- Estudos médicos
- Controle de qualidade
- Pesquisas de mercado
- Estudos científicos em geral
Considerações Importantes
- O intervalo de confiança não indica a probabilidade do parâmetro populacional estar no intervalo.
- A interpretação correta é que, se o processo for repetido muitas vezes, a proporção de intervalos que contêm o verdadeiro parâmetro será aproximadamente igual ao nível de confiança.
- Aumentar o nível de confiança resulta em intervalos mais amplos.
- Para reduzir a margem de erro mantendo o mesmo nível de confiança, é necessário aumentar o tamanho da amostra.
Referências Bibliográficas
- Montgomery, D. C., & Runger, G. C. (2010). Applied Statistics and Probability for Engineers.
- Morettin, P. A., & Bussab, W. O. (2017). Estatística Básica.
- Triola, M. F. (2017). Introdução à Estatística.
- Bezanson, J., Edelman, A., Karpinski, S., & Shah, V. B. (2017). Julia: A fresh approach to numerical computing. SIAM review.
