
A regressão linear é uma das técnicas estatísticas mais utilizadas para modelar a relação entre duas variáveis quantitativas. Ela permite prever o valor de uma variável (dependente) a partir do valor de outra (independente), ajustando uma reta aos dados observados.
O que é Regressão Linear?
A regressão linear simples busca encontrar a melhor reta que descreve a relação entre uma variável explicativa (X) e uma variável resposta (Y). A equação geral é:
\[Y = a + bX + \varepsilon\]- $Y$: variável dependente (resposta)
- $X$: variável independente (explicativa)
- $a$: intercepto (valor de Y quando X = 0)
- $b$: coeficiente angular (inclinação da reta)
- $\varepsilon$: erro aleatório
Exemplo Prático em Julia
Vamos ajustar uma regressão linear simples usando Julia.
using DataFrames, GLM, Plots
# Dados de exemplo: Horas de estudo (X) e Nota na prova (Y)
dados = DataFrame(HorasEstudo = [5, 7, 8, 10, 12, 15, 18, 20],
Nota = [6, 7, 7.5, 8, 8.5, 9, 9.5, 10])
# Ajuste do modelo linear
modelo = lm(@formula(Nota ~ HorasEstudo), dados)
# Resumo do modelo
println(coeftable(modelo))
# Previsão para 14 horas de estudo
pred = predict(modelo, DataFrame(HorasEstudo = [14]))
println("Previsão para 14 horas de estudo: ", pred[1])
# Visualização
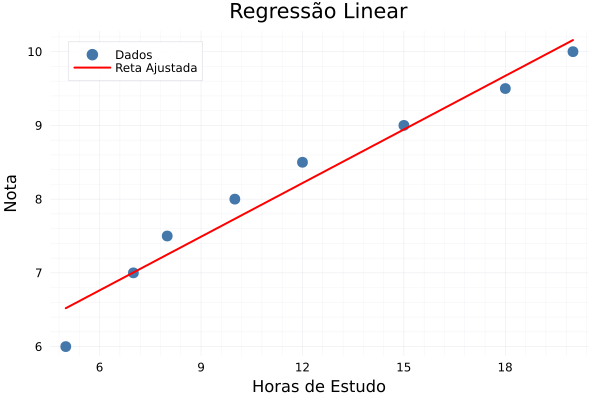
scatter(dados.HorasEstudo, dados.Nota, label="Dados", xlabel="Horas de Estudo", ylabel="Nota", title="Regressão Linear")
plot!(dados.HorasEstudo, predict(modelo), label="Reta Ajustada", lw=2, color=:red)
────────────────────────────────────────────────────────────────────────
Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95%
────────────────────────────────────────────────────────────────────────
(Intercept) 5.30838 0.272462 19.48 <1e-05 4.64169 5.97507
HorasEstudo 0.242452 0.0211233 11.48 <1e-04 0.190765 0.294139
────────────────────────────────────────────────────────────────────────
Previsão para 14 horas de estudo: 8.702711028958717
Interpretação dos Resultados
- Intercepto ($a$): Valor esperado da nota quando HorasEstudo = 0.
- Inclinação ($b$): Variação esperada na nota para cada hora adicional de estudo.
- Valor-p: Indica se o coeficiente é estatisticamente significativo.
- $R^2$ (coeficiente de determinação): Mede o quanto da variação de Y é explicida por X (quanto mais próximo de 1, melhor o ajuste).
Visualização Gráfica
A regressão linear pode ser visualizada como uma reta que “melhor se ajusta” aos pontos do gráfico de dispersão. O objetivo é minimizar a soma dos quadrados dos resíduos (diferença entre valores observados e previstos).
Quando Usar Regressão Linear?
- Quando deseja prever uma variável quantitativa a partir de outra.
- Quando a relação entre as variáveis é aproximadamente linear.
- Quando os resíduos apresentam distribuição aproximadamente normal e variância constante (homocedasticidade).
Dicas e Limitações
- Sempre visualize os dados antes de ajustar o modelo.
- Verifique a presença de outliers e influências.
- Não extrapole previsões para fora do intervalo observado.
- Para múltiplas variáveis explicativas, use regressão linear múltipla.
Resolução Manual Passo a Passo
Vamos resolver o mesmo exemplo da regressão linear (Horas de Estudo vs Nota) manualmente, mostrando todos os cálculos:
Dados
| Horas de Estudo (X) | Nota (Y) |
|---|---|
| 5 | 6 |
| 7 | 7 |
| 8 | 7.5 |
| 10 | 8 |
| 12 | 8.5 |
| 15 | 9 |
| 18 | 9.5 |
| 20 | 10 |
Total de observações: \(n = 8\)
1. Calcule as médias de X e Y
\[\bar{X} = \frac{5 + 7 + 8 + 10 + 12 + 15 + 18 + 20}{8} = \frac{95}{8} = 11,875\] \[\bar{Y} = \frac{6 + 7 + 7,5 + 8 + 8,5 + 9 + 9,5 + 10}{8} = \frac{65,5}{8} = 8,1875\]2. Calcule as somas necessárias
Vamos calcular \(\sum X_i\), \(\sum Y_i\), \(\sum X_i^2\), \(\sum Y_i^2\), \(\sum X_i Y_i\):
| Xi | Yi | Xi2 | Yi2 | XiYi |
|---|---|---|---|---|
| 5 | 6 | 25 | 36 | 30 |
| 7 | 7 | 49 | 49 | 49 |
| 8 | 7.5 | 64 | 56.25 | 60 |
| 10 | 8 | 100 | 64 | 80 |
| 12 | 8.5 | 144 | 72.25 | 102 |
| 15 | 9 | 225 | 81 | 135 |
| 18 | 9.5 | 324 | 90.25 | 171 |
| 20 | 10 | 400 | 100 | 200 |
| 95 | 40 | 1331 | 330 | 827 |
3. Calcule a variância de X e a covariância entre X e Y
A fórmula para o coeficiente angular (\(b\)) é:
\[b = \frac{\sum (X_i - \bar{X})(Y_i - \bar{Y})}{\sum (X_i - \bar{X})^2}\]Mas podemos usar a forma equivalente:
\[b = \frac{\sum X_i Y_i - n \bar{X} \bar{Y}}{\sum X_i^2 - n \bar{X}^2}\]Calculando:
\[n \bar{X} \bar{Y} = 8 \times 11,875 \times 8,1875 = 8 \times 97,22265625 = 777,78125\] \[n \bar{X}^2 = 8 \times (11,875)^2 = 8 \times 141,015625 = 1128,125\]Agora:
\[\sum X_i Y_i - n \bar{X} \bar{Y} = 827 - 777,78125 = 49,21875\] \[\sum X_i^2 - n \bar{X}^2 = 1331 - 1128,125 = 202,875\]Portanto:
\[b = \frac{49,21875}{202,875} \approx 0,24245\]4. Calcule o intercepto (\(a\))
\[a = \bar{Y} - b \bar{X} = 8,1875 - 0,24245 \times 11,875 \approx 8,1875 - 2,8805 = 5,3070\]5. Equação da reta ajustada
\[\boxed{Y = 5,31 + 0,24 X}\](Arredondando para duas casas decimais)
6. Previsão para 14 horas de estudo
\[Y = 5,31 + 0,24 \times 14 = 5,31 + 3,36 = 8,67\](Usando mais casas decimais, \(Y = 5,30838 + 0,24245 \times 14 = 5,30838 + 3,3943 = 8,7027\))
7. Interpretação
- Inclinação (\(b\)): Cada hora adicional de estudo aumenta a nota esperada em aproximadamente 0,24 pontos.
- Intercepto (\(a\)): Nota esperada para quem não estuda (\(X=0\)) seria cerca de 5,31.
- Previsão: Para 14 horas de estudo, a nota prevista é aproximadamente 8,70.
Calculadora de Regressão Linear
| X | Y |
|---|
Referências
- Montgomery, D. C., & Peck, E. A. (2012). Introduction to Linear Regression Analysis.
- Draper, N. R., & Smith, H. (1998). Applied Regression Analysis.
- Triola, M. F. (2017). Introdução à Estatística.
