A Análise de Variância (ANOVA) é uma técnica estatística utilizada para comparar médias de dois ou mais grupos e verificar se pelo menos um deles difere significativamente dos demais. É amplamente empregada em experimentos científicos, controle de qualidade, ciências sociais e biológicas.
Breve História da ANOVA
A ANOVA foi desenvolvida pelo estatístico britânico Sir Ronald A. Fisher na década de 1920. Fisher introduziu a técnica em seu trabalho clássico “Statistical Methods for Research Workers” (1925), revolucionando a análise de experimentos agrícolas e, posteriormente, de diversas áreas do conhecimento.
Antes da ANOVA, os métodos estatísticos para comparar mais de dois grupos eram limitados e pouco eficientes. Fisher percebeu que, ao decompor a variabilidade total dos dados em componentes atribuíveis a diferentes fontes (entre grupos e dentro dos grupos), seria possível testar hipóteses sobre médias de vários grupos simultaneamente, sem aumentar o risco de erro tipo I.
A ANOVA rapidamente se tornou uma das ferramentas mais importantes da estatística experimental, sendo fundamental para o avanço do desenho de experimentos e da inferência estatística.
Curiosidade: O termo “variância” também foi cunhado por Fisher, que considerava a decomposição da variância uma das ideias centrais da estatística moderna.

Classes de Modelos na ANOVA
Existem três classes principais de modelos usados na análise de variância:
1. Modelos de Efeitos Fixos
- Definição: Os níveis dos fatores (grupos) analisados são fixos e de interesse específico do pesquisador.
- Exemplo: Comparar o efeito de três fertilizantes específicos (A, B, C) sobre o crescimento de plantas. Só interessam esses fertilizantes, não outros.
- Interpretação: As conclusões valem apenas para os níveis estudados.
2. Modelos de Efeitos Aleatórios
- Definição: Os níveis dos fatores são considerados uma amostra aleatória de uma população maior de possíveis níveis.
- Exemplo: Avaliar a variação entre diferentes lotes de produção, onde os lotes são sorteados de uma grande população de lotes possíveis.
- Interpretação: As conclusões podem ser generalizadas para toda a população de níveis.
3. Modelos Mistos (Efeitos Fixos e Aleatórios)
- Definição: Incluem simultaneamente fatores de efeitos fixos e aleatórios.
- Exemplo: Testar diferentes tratamentos (fixos) em diferentes blocos ou locais (aleatórios).
- Interpretação: Permite avaliar tanto o efeito específico de certos tratamentos quanto a variabilidade geral de blocos ou ambientes.
Resumo:
- Efeitos fixos: interesse nos níveis específicos.
- Efeitos aleatórios: interesse na variabilidade geral.
- Mistos: combinam ambos.
Essas classes de modelos determinam como interpretar os resultados da ANOVA e como generalizar as conclusões do experimento.
Visualizando a lógica da ANOVA: variabilidade entre e dentro dos grupos
using StatsPlots
using DataFrames, Statistics
theme(:bright)
# Função para criar os plots
function criar_plot(titulo, variabilidade_entre, variabilidade_dentro)
# Dados simulados com diferentes variabilidades
df = DataFrame(grupo = repeat(["A", "B", "C"], inner=30),
valor = vcat(randn(30) .* variabilidade_dentro .+ 0,
randn(30) .* variabilidade_dentro .+ variabilidade_entre,
randn(30) .* variabilidade_dentro .+ 2*variabilidade_entre))
# Mapeia grupos para posições numéricas
grupos = unique(df.grupo)
df.jittered_x = [findfirst(==(g), grupos) + 0.07*randn() for g in df.grupo]
# Calcula médias
media_geral = mean(df.valor)
medias_por_grupo = combine(groupby(df, :grupo), :valor => mean => :media)
# Cria o gráfico
p = scatter(df.jittered_x, df.valor,
group = df.grupo,
xticks = (1:length(grupos), grupos),
legend = :none,
alpha = 0.6,
lw = 0,
markersize = 7,
xlabel = "Grupo", ylabel = "Valor",
title = titulo)
# Linha da média geral
plot!(p, [0.5, length(grupos) + 0.5], [media_geral, media_geral],
lw = 2, linestyle = :dash, alpha = 0.6, color = :black, label = "Média Geral")
# Linhas das médias por grupo
for (i, row) in enumerate(eachrow(medias_por_grupo))
plot!(p, [i - 0.3, i + 0.3], [row.media, row.media],
lw = 3, linestyle = :dash, alpha = 0.6, color = :crimson,
label = i == 1 ? "Médias por Grupo" : "")
end
return p
end
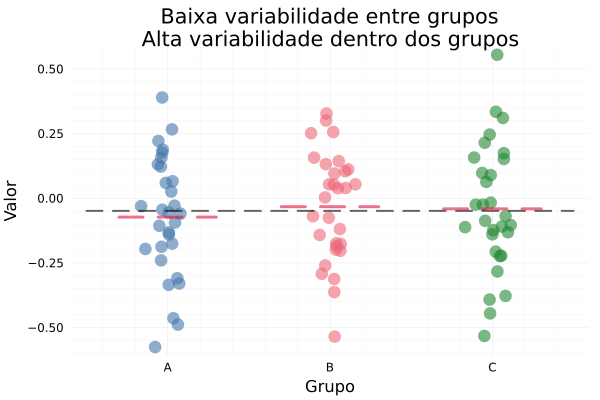
# Plot 1: Baixa variabilidade entre grupos - Alta variabilidade dentro dos grupos
p1 = criar_plot("Baixa variabilidade entre grupos\nAlta variabilidade dentro dos grupos", 0, 0.2)
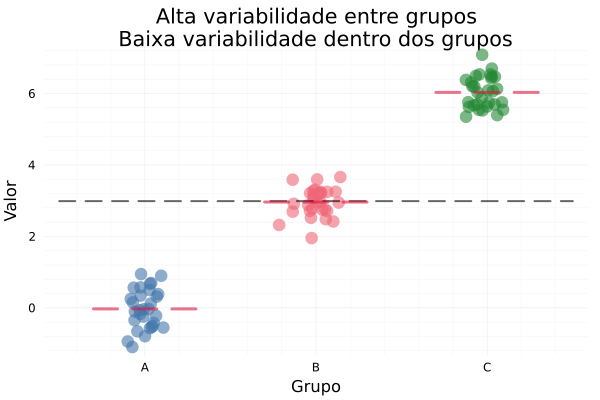
# Plot 2: Alta variabilidade entre grupos - Baixa variabilidade dentro dos grupos
p2 = criar_plot("Alta variabilidade entre grupos\nBaixa variabilidade dentro dos grupos", 3.0, 0.5)
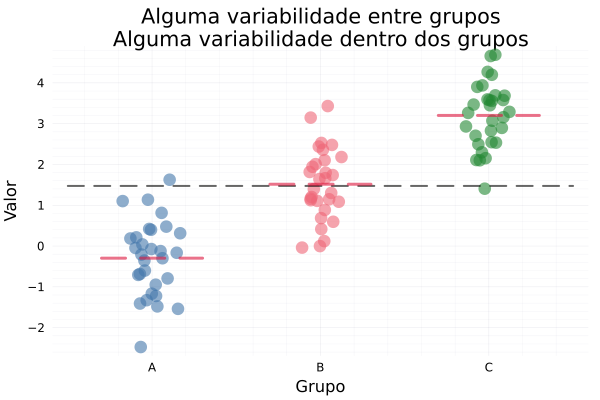
# Plot 3: Alguma variabilidade entre grupos - Alguma variabilidade dentro dos grupos
p3 = criar_plot("Alguma variabilidade entre grupos\nAlguma variabilidade dentro dos grupos", 1.5, 1.0)
# Exibir os plots
display(p1)
display(p2)
display(p3)
Exemplos visuais gerados pelo código acima:
Como esses gráficos ilustram a lógica da ANOVA?
ANOVA é uma técnica estatística usada para comparar médias de três ou mais grupos. Ela testa a hipótese nula de que todas as médias populacionais são iguais.
A ideia central da ANOVA é:
Se a variabilidade entre os grupos for grande em relação à variabilidade dentro dos grupos, é provável que pelo menos um grupo tenha uma média significativamente diferente dos outros.
🎯 Como o exemplo ilustra isso?
A função criar_plot gera gráficos com dados simulados de três grupos (“A”, “B”, “C”), variando os níveis de:
- variabilidade_entre: distância entre as médias dos grupos → está relacionado à variância entre grupos;
- variabilidade_dentro: espalhamento dos valores dentro de cada grupo → está relacionado à variância dentro dos grupos.
🔍 Interpretação dos gráficos
- p1: Baixa variabilidade entre / Alta dentro
- As médias dos grupos são praticamente iguais (0, 0, 0).
- Os dados estão bem espalhados dentro de cada grupo.
- Resultado esperado em uma ANOVA: provavelmente não há diferença significativa entre os grupos.
- p2: Alta variabilidade entre / Baixa dentro
- As médias estão bem separadas (0, 3, 6).
- Pouca variação dentro de cada grupo.
- Resultado esperado em uma ANOVA: diferença significativa entre grupos.
- p3: Variabilidade moderada entre e dentro
- Médias moderadamente diferentes.
- Espalhamento interno também moderado.
- Resultado esperado em uma ANOVA: pode ou não ser significativa, depende da razão F.
⚖️ Relação com o teste F (usado em ANOVA)
A estatística F do teste ANOVA é:
\[F = \frac{\text{Variância entre grupos}}{\text{Variância dentro dos grupos}}\]Os gráficos estão visualizando exatamente essa razão:
- Se $F$ for grande → diferença significativa.
- Se $F$ for próxima de 1 → sem diferença significativa.
✅ Conclusão
Esse exemplo demonstra intuitivamente os princípios da ANOVA, sem calcular diretamente o teste. Ele é excelente para ensino, pois mostra como a diferença entre as médias dos grupos e a variabilidade interna afetam o resultado de um teste ANOVA.
Quando Usar ANOVA?
- Quando deseja comparar médias de três ou mais grupos independentes.
- Quando as variáveis são quantitativas e os grupos são categóricos.
- Quando os pressupostos de normalidade e homocedasticidade são atendidos.
Exemplos de aplicação:
- Comparar rendimento de diferentes fertilizantes em plantações.
- Avaliar desempenho de alunos em diferentes métodos de ensino.
Tipos de ANOVA
- ANOVA One-Way (um fator): Compara médias de grupos definidos por um único fator (ex: tipo de tratamento).
- ANOVA Two-Way (dois fatores): Avalia o efeito de dois fatores e sua interação (ex: tipo de tratamento e sexo).
- ANOVA de medidas repetidas: Para dados em que os mesmos indivíduos são avaliados em diferentes condições.
Pressupostos da ANOVA
- Independência: As observações são independentes entre si.
- Normalidade: Os resíduos (erros) seguem distribuição normal.
- Homocedasticidade: As variâncias dos grupos são iguais.
Dica: Teste de Shapiro-Wilk para normalidade e Levene para homocedasticidade.
Exemplo Prático Manual (Passo a Passo)
Suponha o rendimento (em kg) de três fertilizantes em 5 plantas cada:
- A: 20, 21, 19, 22, 20
- B: 18, 17, 20, 16, 19
- C: 23, 22, 21, 24, 25
Vamos resolver o teste ANOVA one-way completo, passo a passo:
1. Calcule a média de cada grupo
- $\bar{x}_A = \frac{20 + 21 + 19 + 22 + 20}{5} = \frac{102}{5} = 20,4$
- $\bar{x}_B = \frac{18 + 17 + 20 + 16 + 19}{5} = \frac{90}{5} = 18,0$
- $\bar{x}_C = \frac{23 + 22 + 21 + 24 + 25}{5} = \frac{115}{5} = 23,0$
2. Calcule a média geral (sem arredondar)
- $\bar{x}_G = \frac{102 + 90 + 115}{15} = \frac{307}{15} = 20,466666\ldots$
3. Calcule a Soma dos Quadrados Entre Grupos (SQB) usando médias exatas
$SQB = 5 \times [(20,4 - 20,466666\ldots)^2 + (18,0 - 20,466666\ldots)^2 + (23,0 - 20,466666\ldots)^2]$
- $(20,4 - 20,466666\ldots)^2 = ( -0,066666\ldots )^2 = 0,004444\ldots$
- $(18,0 - 20,466666\ldots)^2 = ( -2,466666\ldots )^2 = 6,084444\ldots$
- $(23,0 - 20,466666\ldots)^2 = (2,533333\ldots )^2 = 6,417777\ldots$
$SQB = 5 \times (0,004444\ldots + 6,084444\ldots + 6,417777\ldots ) = 5 \times 12,506666\ldots = 62,533333\ldots$
4. Calcule a Soma dos Quadrados Dentro dos Grupos (SQD)
$SQD = \sum_{i=1}^k \sum_{j=1}^n (x_{ij} - \bar{x}_i)^2$
- Para A:
- $(20-20,4)^2 = 0,16$
- $(21-20,4)^2 = 0,36$
- $(19-20,4)^2 = 1,96$
- $(22-20,4)^2 = 2,56$
- $(20-20,4)^2 = 0,16$
- Soma A: $0,16 + 0,36 + 1,96 + 2,56 + 0,16 = 5,2$
- Para B:
- $(18-18)^2 = 0$
- $(17-18)^2 = 1$
- $(20-18)^2 = 4$
- $(16-18)^2 = 4$
- $(19-18)^2 = 1$
- Soma B: $0 + 1 + 4 + 4 + 1 = 10$
- Para C:
- $(23-23)^2 = 0$
- $(22-23)^2 = 1$
- $(21-23)^2 = 4$
- $(24-23)^2 = 1$
- $(25-23)^2 = 4$
- Soma C: $0 + 1 + 4 + 1 + 4 = 10$
$SQD = 5,2 + 10 + 10 = 25,2$
5. Calcule os graus de liberdade
- Entre grupos: $gl_B = 3 - 1 = 2$
- Dentro dos grupos: $gl_D = 15 - 3 = 12$
6. Calcule os Quadrados Médios (QM)
- $QM_B = 62,533333\ldots / 2 = 31,266666\ldots$
- $QM_D = 25,2 / 12 = 2,1$
7. Calcule a estatística F
$F = 31,266666\ldots / 2,1 = 14,8889$
8. Decisão
- Consulte a tabela F para $gl_B = 2$ e $gl_D = 12$ ao nível de 5%: $F_{crítico} \approx 3,89$
- Como $F_{calculado} = 14,89 > 3,89$, rejeitamos $H_0$.
- O valor-p (calculado pelo software) é $\approx 0,0006$, confirmando a rejeição.
Conclusão:
Há diferença significativa entre as médias dos grupos. Pelo menos um fertilizante tem rendimento diferente dos outros.
Observação: Usando as médias exatas e sem arredondar valores intermediários, o valor da estatística F coincide exatamente com o resultado do Julia: 14,8889.
Exemplo em Julia
using Statistics
using HypothesisTests
using StatsPlots
using DataFrames
using CategoricalArrays
using Measures
theme(:bright)
# Dados
a = [20, 21, 19, 22, 20]
b = [18, 17, 20, 16, 19]
c = [23, 22, 21, 24, 25]
# ANOVA
anova = OneWayANOVATest(a, b, c)
println(anova)
println("Valor-p: ", pvalue(anova))
# Criar DataFrame
df = DataFrame(:Grupo => repeat(["A", "B", "C"], inner=5), :Valor => vcat(a, b, c))
df.Grupo = CategoricalArray(df.Grupo, ordered=true, levels=["A", "B", "C"])
# Calcular médias por grupo
medias = combine(groupby(df, :Grupo), :Valor => mean => :Media)
# X para posição dos grupos no gráfico
x = 1:length(levels(df.Grupo)) # [1, 2, 3]
# Y com médias na ordem dos grupos
y_media = [
medias.Media[findfirst(==("A"), medias.Grupo)],
medias.Media[findfirst(==("B"), medias.Grupo)],
medias.Media[findfirst(==("C"), medias.Grupo)]
]
# Paleta de cores
pal = [:steelblue, :darkseagreen, :orchid]
# Margens ajustadas com Measures.jl para não cortar textos
right_margin = 10mm
left_margin = 5mm
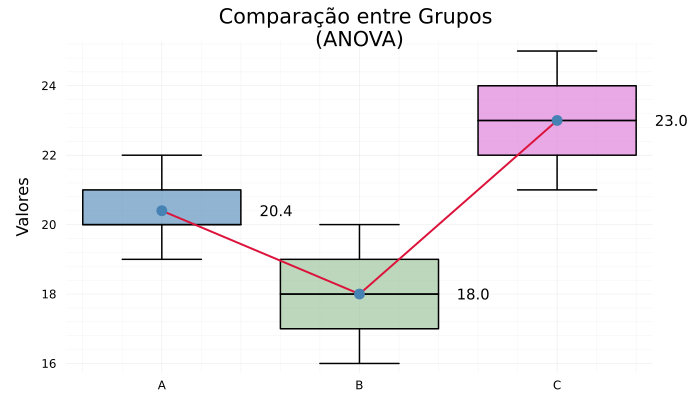
# Criar boxplot com margem direita aumentada
p = @df df boxplot(:Grupo, :Valor,
group = :Grupo,
palette = pal,
title = "Comparação entre Grupos \n(ANOVA)",
ylabel = "Valores",
legend = false,
fillalpha = 0.6,
linecolor = :black,
linewidth = 1.5,
outlier = :circle,
size = (700, 400),
right_margin = right_margin,
left_margin = left_margin)
# Linha conectando as médias
plot!(p, x, y_media, lw=2, marker=:circle, linecolor=:crimson, label="Médias")
# Anotações das médias à direita de cada ponto
for (xi, yi) in zip(x, y_media)
annotate!(p, xi + 0.5, yi, text(string(round(yi, digits=2)), :black, :left, 10))
end
display(p)
One-way analysis of variance (ANOVA) test
-----------------------------------------
Population details:
parameter of interest: Means
value under h_0: "all equal"
point estimate: NaN
Test summary:
outcome with 95% confidence: reject h_0
p-value: 0.0006
Details:
number of observations: [5, 5, 5]
F statistic: 14.8889
degrees of freedom: (2, 12)
Valor-p: 0.0005615849536226485
- Rejeição da hipótese nula (h₀): O teste ANOVA rejeitou a hipótese de que todas as médias dos grupos são iguais ao nível de 5% de significância (95% de confiança). Isso significa que há evidências estatísticas de que pelo menos um dos grupos tem média diferente dos outros.
- Valor-p muito pequeno (0.0006): A probabilidade de observarmos diferenças tão grandes entre as médias dos grupos, caso todas fossem realmente iguais, é de apenas 0,06%. Portanto, é muito improvável que as médias sejam todas iguais.
- Estatística F elevada (14.89): Indica forte evidência contra a hipótese nula.
- O teste ANOVA não indica qual grupo é diferente: Ele apenas aponta que existe diferença significativa. Para identificar onde estão as diferenças, é necessário realizar testes post-hoc, como o teste de Tukey.
Avisos Importantes
- ANOVA indica que há diferença, mas não diz onde está a diferença. Para isso, use testes post-hoc (ex: Tukey).
- Sempre verifique os pressupostos antes de interpretar o resultado.
- Para grupos com variâncias muito diferentes ou dados não normais, use alternativas como Kruskal-Wallis.
Referências Bibliográficas
- Montgomery, D. C., & Runger, G. C. (2010). Applied Statistics and Probability for Engineers.
- Morettin, P. A., & Bussab, W. O. (2017). Estatística Básica.
- Triola, M. F. (2017). Introdução à Estatística.
- Zar, J. H. (2010). Biostatistical Analysis.
