Testes de Hipótese

Ilustração de Teste de Hipótese

Os Testes de Hipótese são procedimentos estatísticos que nos permitem tomar decisões sobre parâmetros populacionais com base em dados amostrais. São ferramentas fundamentais para a inferência estatística e tomada de decisões baseadas em evidências.

🎯 Importante:
Um teste de hipótese envolve duas hipóteses: - A hipótese nula ($H_0$): afirmação inicial que assumimos como verdadeira - A hipótese alternativa ($H_1$ ou $H_a$): afirmação que contradiz $H_0$

1. Conceitos Fundamentais

1.1 Estrutura Básica

Um teste de hipótese segue uma estrutura sistemática:

Formulação das Hipóteses
- Hipótese nula ($H_0$)
- Hipótese alternativa ($H_1$)
Nível de Significância ($\alpha$)
- Probabilidade de erro tipo I
- Geralmente 5% ou 1%
Estatística de Teste
- Medida calculada a partir dos dados
- Base para a decisão
Região Crítica
- Valores que levam à rejeição de $H_0$
- Determinada por $\alpha$

1.2 Tipos de Erro

Decisão vs. Realidade	H₀ Verdadeira	H₀ Falsa
Rejeitar H₀	Erro Tipo I (α)	Decisão Correta
Não Rejeitar H₀	Decisão Correta	Erro Tipo II (β)

🔴 Erro Tipo I (α)

O que é: Rejeitamos $H_0$ mesmo ela sendo verdadeira.
Exemplo: Suponha que um novo medicamento não seja mais eficaz que o atual (ou seja, $H_0$ é verdadeira), mas ao aplicar o teste, os dados indicam falsamente que ele é mais eficaz, levando à rejeição de $H_0$.
Consequência: Assumimos que existe um efeito ou diferença quando na realidade não há.
Probabilidade: Representada por α, geralmente fixada em 5% (0,05).

✅ Decisão Correta (quando H₀ é verdadeira e não a rejeitamos)

O que é: Não rejeitamos $H_0$ e ela realmente é verdadeira.
Exemplo: Um medicamento realmente não é melhor que o outro, e o teste estatístico confirma isso.
Consequência: Decisão correta, sem erro cometido.

✅ Decisão Correta (quando H₀ é falsa e a rejeitamos)

O que é: Rejeitamos $H_0$ e ela de fato é falsa.
Exemplo: Um novo tratamento realmente é mais eficaz, e o teste estatístico detecta essa diferença.
Consequência: Decisão correta, identificando corretamente o efeito.

🔵 Erro Tipo II (β)

O que é: Não rejeitamos $H_0$, mesmo ela sendo falsa.
Exemplo: Um novo método é realmente melhor que o atual, mas o teste não encontra evidências suficientes e $H_0$ não é rejeitada.
Consequência: Perdemos a chance de reconhecer uma melhoria ou efeito real.
Probabilidade: Representada por β. Quanto menor o β, maior o poder do teste (capacidade de detectar um efeito real).

julia

using Plots
using Distributions

# Distribuições
μ0 = 0
μ1 = 1.5
σ = 1
α = 0.05

dist_H0 = Normal(μ0, σ)
dist_H1 = Normal(μ1, σ)

# Valor crítico para teste unilateral (cauda direita)
z_crit = quantile(dist_H0, 1 - α)

# Cálculo do erro tipo II (β) e poder do teste
β = cdf(dist_H1, z_crit)
poder = 1 - β

# Curvas
x = -3:0.01:5
y_H0 = pdf.(dist_H0, x)
y_H1 = pdf.(dist_H1, x)

# Inicia o gráfico com H0 e H1
plot(x, y_H0, label="H₀: N(0,1)", lw=2, color=:steelblue, legend=:topright)
plot!(x, y_H1, label="H₁: N(1.5,1)", lw=2, color=:crimson)

# Área de erro tipo I (α)
fill_x1 = x[x .>= z_crit]
fill_y1 = pdf.(dist_H0, fill_x1)
plot!(fill_x1, fill_y1, fillrange=0, fillalpha=0.4, label="Erro Tipo I (α)", color=:steelblue)

# Área de erro tipo II (β)
fill_x2 = x[x .<= z_crit]
fill_y2 = pdf.(dist_H1, fill_x2)
plot!(fill_x2, fill_y2, fillrange=0, fillalpha=0.4, label="Erro Tipo II (β)", color=:crimson)

# Linha de corte
vline!([z_crit], label="Valor crítico", lw=2, linestyle=:dash, color=:black)

# Anotações
annotate!(z_crit + 0.5, 0.05, text("Área α", :black, 10))
annotate!(z_crit - 1.0, 0.08, text("Área β", :black, 10))
annotate!(μ0, 0.4, text("H₀", :black, 12, :center))
annotate!(μ1, 0.3, text("H₁", :black, 12, :center))

# Adiciona os resultados como curvas invisíveis só para aparecer no legend
plot!([NaN], [NaN], label="Valor crítico: $(round(z_crit, digits=4))")
plot!([NaN], [NaN], label="Erro Tipo II (β): $(round(β, digits=4))")
plot!([NaN], [NaN], label="Poder do teste: $(round(poder, digits=4))")

# Eixos e título
xlabel!("Estatística de teste")
ylabel!("Densidade")
title!("Visualização dos Erros Tipo I (α) e Tipo II (β)")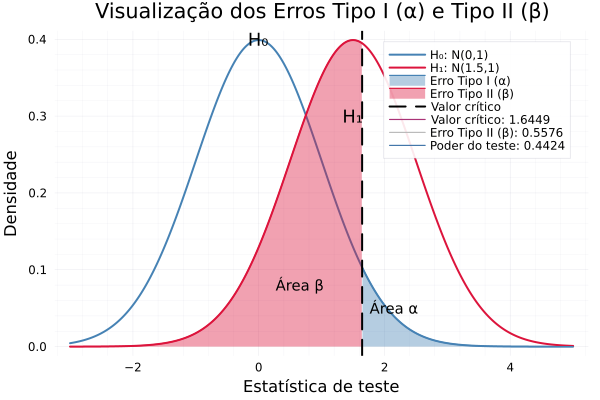

Ilustração de Teste de Hipótese

📌 1. Valor crítico (zₐ = 1.6449)

Esse é o ponto de corte da curva da hipótese nula (H₀) para rejeitar ou não rejeitar a hipótese.

Como o teste é unilateral à direita e o nível de significância é α = 0.05, usamos:

# Saída

z_crit = quantile(Normal(0,1), 1 - α) = quantile(Normal(0,1), 0.95) ≈ 1.6449

Em termos práticos: Se sua estatística de teste (z-calculado) for maior que 1.6449, você rejeita H₀.

📌 2. Erro Tipo II (β = 0.5576)

Esse valor representa a probabilidade de não rejeitar H₀ quando H₁ é verdadeira.

Em outras palavras, é o risco de falhar em detectar um efeito real (ou seja, perder uma descoberta importante).

Aqui: Existe uma probabilidade de 55,76% de você não detectar a diferença real entre H₀ e H₁ (com μ₀ = 0 e μ₁ = 1.5).

📌 3. Poder do teste (1 - β = 0.4424)

O poder do teste representa a capacidade de detectar corretamente um efeito verdadeiro.

Aqui: O teste tem 44,24% de chance de detectar corretamente que H₁ é verdadeira quando ela realmente é.

Em geral, deseja-se um poder ≥ 80% (ou seja, β ≤ 0.20), então: ⚠️ Esse teste está com poder baixo, o que significa que ele não é muito eficaz para detectar a diferença especificada entre μ₀ e μ₁.

🔎 Conclusão interpretativa

Valor	Interpretação
z_crit = 1.6449	Limite a partir do qual rejeitamos H₀
β = 0.5576	Alta chance de errar ao não rejeitar H₀ quando H₁ é verdadeira
Poder = 0.4424	Baixa chance de detectar a verdade (poder fraco)

💡 O que fazer se o poder está baixo?

Você pode:

Aumentar o tamanho da amostra
Aumentar a diferença entre μ₀ e μ₁
Reduzir a variabilidade (σ)
Aceitar um nível de significância α maior (com cuidado)

Ilustração de Teste de Hipótese A imagem acima ilustra, de forma didática e bem-humorada, os quatro possíveis resultados de um teste diagnóstico ou de hipótese, usando o exemplo de um teste de gravidez. Essa estrutura é chamada de matriz de decisão ou matriz de confusão, muito usada em Estatística, Machine Learning e Testes de Hipóteses.

🧠 Matriz de Decisão (Confusão)

Condição Real	Grávida	Não Grávida
Teste diz grávida	✅ Verdadeiro Positivo (VP)	❌ Falso Positivo (FP) - Erro Tipo I
Teste diz não grávida	❌ Falso Negativo (FN) - Erro Tipo II	✅ Verdadeiro Negativo (VN)

🟢 Verdadeiro Positivo (VP): Pessoa está grávida e o teste detecta corretamente.
Exemplo: Mulher grávida, médico diz: “Você está grávida”. Decisão correta.
🟢 Verdadeiro Negativo (VN): Pessoa não está grávida e o teste confirma isso.
Exemplo: Homem idoso, médico diz: “Você não está grávida”. Decisão correta.
🔴 Falso Positivo (FP) – Erro Tipo I: Pessoa não está grávida, mas o teste diz que está.
Exemplo: Homem idoso, médico diz: “Você está grávida”.
Erro tipo I: Rejeita a hipótese nula quando ela é verdadeira.
No contexto de testes de hipótese: Concluímos que há efeito quando não há.
🔴 Falso Negativo (FN) – Erro Tipo II: Pessoa está grávida, mas o teste não detecta.
Exemplo: Mulher grávida, médico diz: “Você não está grávida”.
Erro tipo II: Não rejeita a hipótese nula quando ela é falsa.
No contexto de testes de hipótese: Deixa de detectar um efeito que existe.

📊 Relação com Testes de Hipótese

Termo Estatístico	Interpretação
Hipótese Nula (H₀)	Ex: “A pessoa não está grávida”
Hipótese Alternativa (H₁)	Ex: “A pessoa está grávida”
Erro Tipo I (α)	Rejeitar H₀ quando H₀ é verdadeira (falso positivo)
Erro Tipo II (β)	Não rejeitar H₀ quando H₀ é falsa (falso negativo)
Poder do Teste (1 - β)	Capacidade de detectar corretamente um verdadeiro efeito

✅ Conclusão:
A imagem usa um exemplo extremo e bem-humorado (testar gravidez em um homem idoso) para ilustrar a importância de considerar os erros possíveis em qualquer teste, seja diagnóstico, médico ou estatístico. A matriz de decisão nos ajuda a visualizar os acertos (VP e VN) e os erros (FP e FN), essenciais para avaliar a qualidade e validade de qualquer processo decisório baseado em testes.

2. Etapas do Teste de Hipótese

2.1 Formulação das Hipóteses

julia

using HypothesisTests

# Exemplo: Teste para média populacional
function exemplo_teste_media()
    # Dados simulados
    dados = randn(100) .+ 0.5  # Amostra normal com média 0.5
    
    # Teste t de uma amostra
    teste = OneSampleTTest(dados)
    
    println("Teste t para média populacional")
    println("-------------------------------")
    println("H₀: μ = 0")
    println("H₁: μ ≠ 0")
    println("Estatística t = ", round(test_statistic(teste), digits=4))
    println("Valor-p = ", round(pvalue(teste), digits=4))
end

exemplo_teste_media()

2.2 Escolha do Nível de Significância

O nível de significância ($\alpha$) é a probabilidade máxima aceitável de cometer um erro tipo I:

$\alpha = 0,05$ (5%): Nível comum em ciências sociais
$\alpha = 0,01$ (1%): Usado quando necessária maior confiança
$\alpha = 0,10$ (10%): Usado em estudos preliminares

2.3 Cálculo da Estatística de Teste

A estatística de teste é uma medida padronizada que segue uma distribuição conhecida sob $H_0$:

Teste Z $Z = \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}$
Teste t $t = \frac{\bar{X} - \mu_0}{s/\sqrt{n}}$
Teste Qui-quadrado $\chi^2 = \sum_{i=1}^k \frac{(O_i - E_i)^2}{E_i}$

3. Valor-p e Tomada de Decisão

3.1 Interpretação do Valor-p

Interpretação do valor-p

Figura: Representação gráfica do valor-p em uma distribuição normal

O valor-p é a probabilidade de obter uma estatística de teste tão ou mais extrema que a observada, assumindo $H_0$ verdadeira:

Se valor-p $\leq \alpha$: Rejeita-se $H_0$
Se valor-p $> \alpha$: Não se rejeita $H_0$

3.2 Poder do Teste

O poder do teste ($1-\beta$) é a probabilidade de rejeitar $H_0$ quando ela é falsa:

julia

using Distributions

function calcular_poder_teste()
    # Parâmetros
    n = 30  # Tamanho da amostra
    α = 0.05  # Nível de significância
    μ₀ = 0  # Média sob H₀
    μₐ = 0.5  # Média sob H₁
    σ = 1  # Desvio padrão
    
    # Valor crítico
    z_crit = quantile(Normal(), 1-α/2)
    
    # Poder do teste
    β = cdf(Normal(), z_crit - (μₐ-μ₀)/(σ/√n)) - 
        cdf(Normal(), -z_crit - (μₐ-μ₀)/(σ/√n))
    poder = 1 - β
    
    println("Análise do Poder do Teste")
    println("-------------------------")
    println("Tamanho da amostra = ", n)
    println("Nível de significância = ", α)
    println("Poder do teste = ", round(poder, digits=4))
end

calcular_poder_teste()

4. Tipos de Testes de Hipótese

4.1 Testes Paramétricos

Teste Z
- Para médias com σ conhecido
- Amostras grandes (n ≥ 30)
Teste t
- Para médias com σ desconhecido
- Uma ou duas amostras
- Amostras pareadas
Teste F
- Comparação de variâncias
- ANOVA

4.2 Testes Não-Paramétricos

Teste de Wilcoxon
- Alternativa ao teste t
- Não assume normalidade
Teste de Mann-Whitney
- Comparação de duas populações
- Dados ordinais
Teste Qui-quadrado
- Independência
- Aderência

5. Exercícios Resolvidos

5.1 Teste para Média Populacional

Exemplo de teste de hipótese

Figura: Distribuição amostral e regiões críticas

Problema: Uma empresa afirma que o tempo médio de atendimento ao cliente é de 10 minutos. Um analista coletou uma amostra de 36 atendimentos e encontrou uma média de 11,2 minutos com desvio padrão de 2,4 minutos. Ao nível de significância de 5%, há evidências para rejeitar a afirmação da empresa?

Dados:

$H_0: \mu = 10$ minutos
$H_1: \mu \neq 10$ minutos
$\bar{x} = 11,2$ minutos
$s = 2,4$ minutos
\[n = 36\]
\[\alpha = 0,05\]

Solução:

Estatística de teste: $t = \frac{\bar{x} - \mu_0}{s/\sqrt{n}} = \frac{11,2 - 10}{2,4/\sqrt{36}} = 3$
Valor crítico (bilateral): $t_{0,025;35} = \pm 2,03$
Decisão: Como |3| > 2,03, rejeitamos $H_0$.

julia

function teste_tempo_atendimento()
    # Dados
    x̄ = 11.2  # Média amostral
    μ₀ = 10.0  # Média sob H₀
    s = 2.4    # Desvio padrão amostral
    n = 36     # Tamanho da amostra
    α = 0.05   # Nível de significância
    
    # Estatística t
    t_stat = (x̄ - μ₀)/(s/√n)
    
    # Valor crítico
    t_crit = quantile(TDist(n-1), 1-α/2)
    
    # Valor-p
    p_valor = 2 * (1 - cdf(TDist(n-1), abs(t_stat)))
    
    println("Teste t para Tempo de Atendimento")
    println("--------------------------------")
    println("Estatística t = ", round(t_stat, digits=4))
    println("Valor crítico = ±", round(t_crit, digits=4))
    println("Valor-p = ", round(p_valor, digits=4))
end

teste_tempo_atendimento()

5.2 Teste de Independência

Problema: Em um estudo sobre a relação entre gênero e preferência por tipo de exercício físico, foram coletados os seguintes dados:

	Musculação	Cardio	Yoga
Masculino	30	15	5
Feminino	20	25	15

Teste se há independência entre gênero e preferência por exercício ao nível de 5% de significância.

Solução:

Hipóteses:
- $H_0$: Gênero e preferência são independentes
- $H_1$: Existe associação entre gênero e preferência
Frequências esperadas: $E_{ij} = \frac{(total_{\text{linha } i})(total_{\text{coluna } j})}{total_{\text{geral}}}$
Estatística qui-quadrado: $\chi^2 = \sum_{i=1}^r \sum_{j=1}^c \frac{(O_{ij} - E_{ij})^2}{E_{ij}}$

julia

function teste_independencia()
    # Dados observados
    O = [30 15 5;
         20 25 15]
    
    # Totais
    n = sum(O)
    r_tot = sum(O, dims=2)
    c_tot = sum(O, dims=1)
    
    # Frequências esperadas
    E = (r_tot * c_tot) / n
    
    # Estatística qui-quadrado
    χ² = sum((O .- E).^2 ./ E)
    
    # Graus de liberdade
    gl = (size(O,1)-1) * (size(O,2)-1)
    
    # Valor-p
    p_valor = 1 - cdf(Chisq(gl), χ²)
    
    println("Teste Qui-quadrado de Independência")
    println("---------------------------------")
    println("Estatística χ² = ", round(χ², digits=4))
    println("Graus de liberdade = ", gl)
    println("Valor-p = ", round(p_valor, digits=4))
end

teste_independencia()

6. Considerações Práticas

6.1 Pressupostos

Normalidade
- Teste de Shapiro-Wilk
- QQ-plot
Independência
- Aleatoriedade da amostra
- Ausência de autocorrelação
Homocedasticidade
- Teste de Levene
- Teste F

6.2 Tamanho da Amostra

O tamanho da amostra afeta:

Poder do teste
Precisão das estimativas
Validade dos pressupostos

7. Intervalos de Confiança e Testes de Hipótese

7.1 Relação com Intervalos de Confiança

Os intervalos de confiança e testes de hipótese são complementares:

Um intervalo de confiança de (1-α)% corresponde a todos os valores de μ₀ que não seriam rejeitados em um teste de nível α
O intervalo fornece mais informação que o teste, pois indica a faixa de valores plausíveis para o parâmetro

7.2 Construção de Intervalos

Para uma média populacional:

\[IC_{1-\alpha} = \bar{x} \pm t_{\alpha/2, n-1} \frac{s}{\sqrt{n}}\]

julia

function calcular_ic_media()
    # Dados
    dados = randn(30) .+ 2  # Amostra com média ≈ 2
    α = 0.05
    
    # Estatísticas
    x̄ = mean(dados)
    s = std(dados)
    n = length(dados)
    
    # Valor crítico t
    t_crit = quantile(TDist(n-1), 1-α/2)
    
    # Intervalo de confiança
    margem_erro = t_crit * (s/√n)
    ic_inf = x̄ - margem_erro
    ic_sup = x̄ + margem_erro
    
    println("Intervalo de Confiança (95%)")
    println("----------------------------")
    println("Limite inferior: ", round(ic_inf, digits=4))
    println("Limite superior: ", round(ic_sup, digits=4))
end

calcular_ic_media()

8. Exemplos Práticos Adicionais

8.1 Teste para Proporção

Problema: Uma empresa de marketing digital afirma que sua nova estratégia de e-mail marketing tem taxa de conversão de 15%. Em uma amostra de 200 e-mails enviados, 40 resultaram em conversão. Teste esta afirmação ao nível de 5% de significância.

Solução:

Hipóteses:
- H₀: p = 0,15
- H₁: p ≠ 0,15
Estatística de teste: $Z = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}$

julia

function teste_proporcao()
    # Dados
    n = 200        # Tamanho da amostra
    x = 40         # Sucessos
    p₀ = 0.15      # Proporção sob H₀
    α = 0.05       # Nível de significância
    
    # Proporção amostral
    p̂ = x/n
    
    # Estatística Z
    z_stat = (p̂ - p₀)/√(p₀*(1-p₀)/n)
    
    # Valor-p
    p_valor = 2 * (1 - cdf(Normal(), abs(z_stat)))
    
    println("Teste Z para Proporção")
    println("---------------------")
    println("Proporção amostral = ", round(p̂, digits=4))
    println("Estatística Z = ", round(z_stat, digits=4))
    println("Valor-p = ", round(p_valor, digits=4))
end

teste_proporcao()

8.2 Teste de Correlação

Problema: Queremos verificar se existe correlação significativa entre as horas de estudo e as notas dos alunos.

julia

function teste_correlacao()
    # Dados simulados
    horas = [2, 3, 4, 3, 5, 6, 4, 5, 6, 7]
    notas = [65, 70, 75, 68, 80, 85, 72, 78, 88, 90]
    
    # Coeficiente de correlação
    r = cor(horas, notas)
    
    # Estatística t
    n = length(horas)
    t_stat = r * √((n-2)/(1-r^2))
    
    # Valor-p
    p_valor = 2 * (1 - cdf(TDist(n-2), abs(t_stat)))
    
    println("Teste de Correlação")
    println("------------------")
    println("Correlação = ", round(r, digits=4))
    println("Estatística t = ", round(t_stat, digits=4))
    println("Valor-p = ", round(p_valor, digits=4))
end

teste_correlacao()

9. Erros Comuns e Boas Práticas

9.1 Erros Comuns

Interpretação Incorreta do Valor-p
- O valor-p NÃO é a probabilidade de H₀ ser verdadeira
- O valor-p é a probabilidade de obter dados tão ou mais extremos que os observados, assumindo H₀ verdadeira
Confusão entre Significância Estatística e Prática
- Significância estatística não implica relevância prática
- Com amostras muito grandes, diferenças pequenas podem ser estatisticamente significativas
Múltiplos Testes sem Correção
- Realizar múltiplos testes aumenta a chance de erro tipo I
- Use correções como Bonferroni ou controle FDR

9.2 Boas Práticas

Planejamento do Estudo
- Defina hipóteses antes da coleta de dados
- Calcule o tamanho da amostra necessário
- Estabeleça critérios de significância prática
Análise de Dados
- Verifique pressupostos antes do teste
- Use visualizações para complementar a análise
- Reporte intervalos de confiança junto com valores-p
Comunicação dos Resultados
- Apresente estatísticas descritivas
- Reporte tamanhos de efeito
- Discuta limitações do estudo

10. Recursos Adicionais

10.1 Ferramentas Online

10.2 Pacotes Estatísticos

R
- stats
- pwr
- coin
Python
- scipy.stats
- statsmodels
- pingouin
Julia
- HypothesisTests.jl
- StatisticalTests.jl
- Power.jl

11. Guia para Escolha do Teste Estatístico

11.1 Árvore de Decisão

Árvore de decisão para escolha de testes

Figura: Árvore de decisão para seleção do teste estatístico apropriado

11.2 Critérios de Seleção

Tipo de Variável

Tipo de Variável	Exemplos	Testes Apropriados
Nominal	Gênero, Cor	Qui-quadrado, Teste exato de Fisher
Ordinal	Escala Likert	Mann-Whitney, Kruskal-Wallis
Intervalar/Razão	Altura, Peso	Teste t, ANOVA

Número de Grupos

Número de Grupos	Paramétrico	Não-Paramétrico
2 grupos independentes	Teste t independente	Mann-Whitney
2 grupos pareados	Teste t pareado	Wilcoxon
> 2 grupos independentes	ANOVA	Kruskal-Wallis
> 2 grupos pareados	ANOVA medidas repetidas	Friedman

Pressupostos dos Testes

🔍 Verificação de Pressupostos: - Normalidade: Shapiro-Wilk ou Kolmogorov-Smirnov - Homocedasticidade: Levene ou Bartlett - Independência: Durbin-Watson

11.3 Fluxograma de Decisão por Objetivo

11.3.1 Comparação de Médias/Medianas

graph TD
    A[Dados Numéricos] --> B{Normal?}
    B -->|Sim| C{Quantos grupos?}
    B -->|Não| D{Quantos grupos?}
    C -->|2 grupos| E{Pareado?}
    C -->|>2 grupos| F{Pareado?}
    D -->|2 grupos| G{Pareado?}
    D -->|>2 grupos| H{Pareado?}
    E -->|Sim| I[Teste t pareado]
    E -->|Não| J[Teste t independente]
    F -->|Sim| K[ANOVA medidas repetidas]
    F -->|Não| L[ANOVA one-way]
    G -->|Sim| M[Wilcoxon]
    G -->|Não| N[Mann-Whitney]
    H -->|Sim| O[Friedman]
    H -->|Não| P[Kruskal-Wallis]

11.3.2 Análise de Relações

graph TD
    A[Tipo de Relação] --> B{Variáveis Numéricas?}
    B -->|Ambas| C{Normal?}
    B -->|Uma Categórica| D[Análise de Grupos]
    B -->|Ambas Categóricas| E[Qui-quadrado/Fisher]
    C -->|Sim| F[Correlação de Pearson]
    C -->|Não| G[Correlação de Spearman]
    D --> H{Normal?}
    H -->|Sim| I[Teste t/ANOVA]
    H -->|Não| J[Mann-Whitney/Kruskal-Wallis]

11.4 Tabela de Decisão Rápida

Objetivo	Condições	Teste Recomendado
Comparar média com valor de referência	Normal	Teste t uma amostra
Comparar média com valor de referência	Não normal	Wilcoxon uma amostra
Comparar duas médias (independentes)	Normal + Variâncias iguais	Teste t independente
Comparar duas médias (independentes)	Normal + Variâncias diferentes	Welch t-test
Comparar duas médias (pareadas)	Normal	Teste t pareado
Comparar > 2 médias	Normal + Homocedástico	ANOVA
Comparar proporções	n grande	Teste Z proporções
Comparar proporções	n pequeno	Teste exato de Fisher
Verificar independência	Categóricas	Qui-quadrado
Avaliar correlação	Normal bivariada	Pearson
Avaliar correlação	Não normal	Spearman

11.5 Exemplos Práticos de Seleção

Exemplo: Eficácia de Medicamento
- Variável: Pressão arterial (numérica)
- Grupos: Antes e depois (pareado)
- Distribuição: Normal
- Teste escolhido: Teste t pareado
Exemplo: Preferência por Marca
- Variável: Escolha de marca (categórica)
- Grupos: Múltiplas marcas
- Teste escolhido: Qui-quadrado

julia

using HypothesisTests

function exemplo_selecao_teste()
    # Exemplo 1: Teste t pareado
    antes = [120, 122, 118, 125, 124]
    depois = [115, 118, 112, 120, 119]
    
    # Teste de normalidade primeiro
    println("Teste de Normalidade (diferenças):")
    dif = depois .- antes
    normal_test = ShapiroWilkTest(dif)
    println("p-valor = ", round(pvalue(normal_test), digits=4))
    
    # Se normal, proceder com teste t pareado
    if pvalue(normal_test) > 0.05
        paired_test = OneSampleTTest(dif)
        println("\nTeste t Pareado:")
        println("Estatística t = ", round(test_statistic(paired_test), digits=4))
        println("p-valor = ", round(pvalue(paired_test), digits=4))
    else
        # Se não normal, usar Wilcoxon
        wilcox_test = SignedRankTest(depois, antes)
        println("\nTeste de Wilcoxon:")
        println("p-valor = ", round(pvalue(wilcox_test), digits=4))
    end
end

exemplo_selecao_teste()

11.6 Considerações Importantes

Tamanho da Amostra
- n < 30: Verificar normalidade é crucial
- n ≥ 30: Testes paramétricos são mais robustos
Violação de Pressupostos
- Leve: Testes paramétricos ainda são robustos
- Severa: Optar por alternativas não-paramétricas
Poder Estatístico
- Testes paramétricos: Maior poder se pressupostos atendidos
- Testes não-paramétricos: Mais seguros se dúvida sobre pressupostos
Interpretabilidade
- Considerar a facilidade de interpretação
- Balancear rigor estatístico com praticidade

12. Testes Paramétricos vs. Não Paramétricos

12.1 Testes Paramétricos

Os testes paramétricos são procedimentos estatísticos que assumem que os dados seguem uma distribuição de probabilidade específica (geralmente a distribuição normal) e fazem inferências sobre os parâmetros dessa distribuição.

12.1.1 Características Principais

Pressupostos
- Normalidade dos dados
- Homogeneidade das variâncias (homocedasticidade)
- Independência das observações
- Variáveis contínuas ou intervalares
Vantagens
- Maior poder estatístico quando os pressupostos são atendidos
- Estimativas mais precisas
- Capacidade de fazer inferências sobre parâmetros populacionais

Exemplos de Testes Paramétricos

Teste	Uso	Pressuposto Principal
Teste t	Comparação de médias	Normalidade
ANOVA	Comparação de múltiplas médias	Normalidade e homocedasticidade
Correlação de Pearson	Associação linear	Normalidade bivariada
Regressão Linear	Relação entre variáveis	Normalidade dos resíduos

12.1.2 Verificação de Pressupostos

julia

using HypothesisTests
using Statistics

function verificar_pressupostos()
    # Dados simulados
    dados = randn(30) .* 2 .+ 1
    
    # 1. Teste de Normalidade
    normalidade = ShapiroWilkTest(dados)
    
    # 2. Teste de Homocedasticidade (entre dois grupos)
    grupo1 = randn(20) .* 2
    grupo2 = randn(20) .* 2
    homog = VarianceFTest(grupo1, grupo2)
    
    println("Verificação de Pressupostos")
    println("---------------------------")
    println("Teste de Normalidade:")
    println("Estatística W = ", round(test_statistic(normalidade), digits=4))
    println("p-valor = ", round(pvalue(normalidade), digits=4))
    println("\nTeste de Homocedasticidade:")
    println("Estatística F = ", round(test_statistic(homog), digits=4))
    println("p-valor = ", round(pvalue(homog), digits=4))
end

verificar_pressupostos()

12.2 Testes Não Paramétricos

Os testes não paramétricos são procedimentos estatísticos que não exigem pressupostos sobre a distribuição dos dados. São também conhecidos como “testes livres de distribuição”.

12.2.1 Características Principais

Vantagens
- Mais flexíveis quanto à distribuição dos dados
- Robustos a outliers
- Aplicáveis a dados ordinais
- Úteis para amostras pequenas
Limitações
- Menor poder estatístico que testes paramétricos
- Não fazem inferências sobre parâmetros específicos
- Podem perder informação ao usar ranks

Exemplos de Testes Não Paramétricos

Teste Não Paramétrico	Equivalente Paramétrico	Uso
Mann-Whitney U	Teste t independente	Comparar dois grupos
Wilcoxon	Teste t pareado	Comparar medidas repetidas
Kruskal-Wallis	ANOVA one-way	Comparar múltiplos grupos
Spearman	Correlação de Pearson	Correlação por ranks

12.2.2 Exemplo Comparativo

julia

function comparar_testes()
    # Dados não normais (distribuição exponencial)
    grupo1 = rand(Exponential(1), 20)
    grupo2 = rand(Exponential(1.5), 20)
    
    # Teste paramétrico (t)
    teste_t = UnequalVarianceTTest(grupo1, grupo2)
    
    # Teste não paramétrico (Mann-Whitney)
    teste_mw = MannWhitneyUTest(grupo1, grupo2)
    
    println("Comparação entre Testes")
    println("----------------------")
    println("Teste t:")
    println("Estatística t = ", round(test_statistic(teste_t), digits=4))
    println("p-valor = ", round(pvalue(teste_t), digits=4))
    println("\nTeste de Mann-Whitney:")
    println("Estatística U = ", round(test_statistic(teste_mw), digits=4))
    println("p-valor = ", round(pvalue(teste_mw), digits=4))
end

comparar_testes()

12.3 Quando Usar Cada Tipo de Teste?

12.3.1 Use Testes Paramétricos Quando:

Dados Atendem aos Pressupostos
- Distribuição normal ou aproximadamente normal
- Variâncias homogêneas
- Tamanho amostral adequado (n ≥ 30)
Precisão é Crucial
- Necessidade de estimativas precisas
- Inferências sobre parâmetros populacionais
- Poder estatístico é prioridade

12.3.2 Use Testes Não Paramétricos Quando:

Violação de Pressupostos
- Dados não normais
- Heteroscedasticidade
- Presença de outliers significativos
Características dos Dados
- Amostra pequena (n < 30)
- Dados ordinais ou rankings
- Distribuição muito assimétrica

⚠️ Dica Importante:
Em caso de dúvida entre teste paramétrico e não paramétrico: 1. Verifique os pressupostos rigorosamente 2. Se houver violação moderada, o teste paramétrico ainda pode ser usado 3. Se houver violação severa, opte pelo teste não paramétrico 4. Considere reportar ambos os resultados se forem divergentes

12.4 Tabela Comparativa Detalhada

Aspecto	Testes Paramétricos	Testes Não Paramétricos
Pressupostos	Mais rigorosos	Mais flexíveis
Poder Estatístico	Maior (quando pressupostos atendidos)	Menor
Robustez	Menor	Maior
Interpretação	Mais direta	Menos intuitiva
Tamanho Amostral	Preferível n ≥ 30	Funciona bem com n < 30
Tipo de Dados	Intervalares/Razão	Qualquer tipo
Outliers	Sensível	Robusto
Precisão	Maior	Menor

12.5 Exemplos de Aplicação

Cenário: Dados Normais, n = 50
- Escolha: Teste paramétrico
- Razão: Pressupostos atendidos, maior poder
Cenário: Dados Assimétricos, n = 15
- Escolha: Teste não paramétrico
- Razão: Amostra pequena, não normalidade
Cenário: Escala Likert
- Escolha: Teste não paramétrico
- Razão: Dados ordinais
Cenário: Medidas Físicas, n = 100
- Escolha: Teste paramétrico
- Razão: Dados contínuos, amostra grande

Quiz Interativo: Teste seus conhecimentos!

🎮 Experimente o quiz sobre Testes de Hipótese:

Se o quiz não carregar, clique aqui para abrir em nova aba.

Referências Adicionais

Wasserman, L. All of Statistics: A Concise Course in Statistical Inference. Springer, 2004.
Lehmann, E. L.; Romano, J. P. Testing Statistical Hypotheses. 3ª ed. Springer, 2005.
Rice, J. A. Mathematical Statistics and Data Analysis. 3ª ed. Thomson Brooks/Cole, 2007.
Efron, B.; Hastie, T. Computer Age Statistical Inference. Cambridge University Press, 2016.
Good, P. I.; Hardin, J. W. Common Errors in Statistics (and How to Avoid Them). 4ª ed. Wiley, 2012.

Morrison Külsenn

Estatística Pura

Testes de Hipótese

1. Conceitos Fundamentais

1.1 Estrutura Básica

1.2 Tipos de Erro

🔴 Erro Tipo I (α)

✅ Decisão Correta (quando H₀ é verdadeira e não a rejeitamos)

✅ Decisão Correta (quando H₀ é falsa e a rejeitamos)

🔵 Erro Tipo II (β)

📌 1. Valor crítico (zₐ = 1.6449)

📌 2. Erro Tipo II (β = 0.5576)

📌 3. Poder do teste (1 - β = 0.4424)

🔎 Conclusão interpretativa

🧠 Matriz de Decisão (Confusão)

📊 Relação com Testes de Hipótese

2. Etapas do Teste de Hipótese

2.1 Formulação das Hipóteses

2.2 Escolha do Nível de Significância

2.3 Cálculo da Estatística de Teste

3. Valor-p e Tomada de Decisão

3.1 Interpretação do Valor-p

3.2 Poder do Teste

4. Tipos de Testes de Hipótese

4.1 Testes Paramétricos

4.2 Testes Não-Paramétricos

5. Exercícios Resolvidos

5.1 Teste para Média Populacional

5.2 Teste de Independência

6. Considerações Práticas

6.1 Pressupostos

6.2 Tamanho da Amostra

7. Intervalos de Confiança e Testes de Hipótese

7.1 Relação com Intervalos de Confiança

7.2 Construção de Intervalos

8. Exemplos Práticos Adicionais

8.1 Teste para Proporção

8.2 Teste de Correlação

9. Erros Comuns e Boas Práticas

9.1 Erros Comuns

9.2 Boas Práticas

10. Recursos Adicionais

10.1 Ferramentas Online

10.2 Pacotes Estatísticos

11. Guia para Escolha do Teste Estatístico

11.1 Árvore de Decisão

11.2 Critérios de Seleção

11.3 Fluxograma de Decisão por Objetivo

11.3.1 Comparação de Médias/Medianas

11.3.2 Análise de Relações

11.4 Tabela de Decisão Rápida

11.5 Exemplos Práticos de Seleção

11.6 Considerações Importantes

12. Testes Paramétricos vs. Não Paramétricos

12.1 Testes Paramétricos

12.1.1 Características Principais

12.1.2 Verificação de Pressupostos

12.2 Testes Não Paramétricos

12.2.1 Características Principais

12.2.2 Exemplo Comparativo

12.3 Quando Usar Cada Tipo de Teste?

12.3.1 Use Testes Paramétricos Quando:

12.3.2 Use Testes Não Paramétricos Quando:

12.4 Tabela Comparativa Detalhada

12.5 Exemplos de Aplicação

Quiz Interativo: Teste seus conhecimentos!

Referências Adicionais

Morrison Külsenn

Estatística Pura