A Análise Exploratória de Dados (AED) é uma abordagem para analisar conjuntos de dados com o objetivo de resumir suas principais características, frequentemente com métodos visuais. Ela ajuda a entender os dados, identificar padrões, detectar anomalias e formular hipóteses.
John Tukey e o Nascimento da AED
A Análise Exploratória de Dados, como a conhecemos hoje, tem suas raízes no trabalho pioneiro de John Wilder Tukey (1915-2000), um dos estatísticos mais influentes do século XX. Tukey, que também era químico e cientista da computação, revolucionou a forma como os dados são analisados e interpretados.
Quem foi John Tukey?
- Nascimento: 16 de junho de 1915, em New Bedford, Massachusetts, EUA
- Formação: Bacharel em Química pela Brown University (1936) e Ph.D. em Matemática pela Princeton University (1939)
- Carreira: Professor em Princeton e pesquisador sênior nos Bell Labs
- Contribuições: Além da AED, Tukey cunhou termos como “bit” (binary digit) e “software”

John Wilder Tukey (1915-2000), o pai da Análise Exploratória de Dados
A Revolução da Análise Exploratória
Em 1977, Tukey publicou o livro seminal “Exploratory Data Analysis”, que estabeleceu os fundamentos da AED. Nesta obra, ele argumentou que a análise estatística não deveria se limitar a testar hipóteses (análise confirmatória), mas também deveria explorar os dados para descobrir padrões inesperados e gerar novas hipóteses.
Princípios Fundamentais de Tukey:
-
Ênfase na Visualização: Tukey acreditava que “a imagem mais simples possível de uma imagem é a melhor, desde que faça o que precisa ser feito”.
-
Resistência: Desenvolveu técnicas robustas que não são afetadas por valores atípicos, como a mediana e os quartis.
-
Exploração Ativa: Encorajava os analistas a “brincar” com os dados, fazendo diferentes perguntas e visualizações.
-
Ferramentas Inovadoras: Criou várias ferramentas visuais que são padrão hoje, incluindo:
- Boxplot (ou diagrama de caixa)
- Stem-and-leaf plot (diagrama de ramo-e-folhas)
- Five-number summary (resumo dos cinco números)
Impacto e Legado
A abordagem de Tukey teve um impacto profundo em diversos campos:
- Ciência de Dados Moderna: A AED é considerada a primeira etapa essencial em qualquer projeto de ciência de dados.
- Big Data: Os princípios de visualização e exploração são ainda mais críticos na era dos grandes volumes de dados.
- Educação: A AED é ensinada em cursos de estatística e ciência de dados em todo o mundo.
A AED Hoje
Embora os princípios fundamentais permaneçam os mesmos, a AED evoluiu com a tecnologia:
- Ferramentas Modernas: Softwares como Python, R e Julia incorporam os princípios de Tukey em suas bibliotecas de visualização.
- Visualizações Interativas: Ferramentas como Tableau e Power BI permitem exploração dinâmica de dados.
- Automação: Técnicas de aprendizado de máquina estão sendo usadas para automatizar partes do processo exploratório.
A visão de Tukey de que “o objetivo mais importante da análise de dados é descobrir o que você não estava procurando” continua a guiar analistas e cientistas de dados em todo o mundo.
Objetivos da Análise Exploratória
- Entender a estrutura e distribuição dos dados
- Identificar valores atípicos e anomalias
- Descobrir padrões e relações entre variáveis
- Validar suposições iniciais
- Preparar os dados para análises mais avançadas
Técnicas Básicas de AED
1. Estatísticas Descritivas
As medidas de tendência central e dispersão fornecem um resumo numérico dos dados:
- Média, mediana e moda
- Amplitude, variância e desvio padrão
- Assimetria e curtose
2. Visualizações Básicas
- Histogramas: Mostram a distribuição de uma variável contínua
- Gráficos de caixa (boxplots): Mostram a distribuição e identificam outliers
- Gráficos de dispersão: Mostram a relação entre duas variáveis
- Gráficos de barras: Úteis para variáveis categóricas
Exemplo Prático em Julia
Vamos realizar uma análise exploratória em um conjunto de dados de exemplo usando Julia. Usaremos o pacote DataFrames para manipulação de dados e Plots para visualização.
Carregando os Pacotes
# Carregando os pacotes necessários
using DataFrames
using Statistics
using Plots
# Criando um conjunto de dados de exemplo com valores estáticos
function criar_dados_estudantes()
# Dados estáticos para garantir reprodutibilidade
nomes = ["Ana", "Carlos", "Maria", "João", "Julia", "Pedro", "Luiza", "Rafael"]
idades = [18, 24, 20, 22, 19, 21, 23, 18] # Idades fixas
notas = [7, 6, 9, 8, 7, 5, 8, 6] # Notas fixas
horas_estudo = [17, 18, 15, 12, 19, 10, 14, 16] # Horas de estudo fixas
aprovado = [nota >= 7 ? "Sim" : "Não" for nota in notas] # Calculado baseado nas notas fixas
return DataFrame(
Nome = nomes,
Idade = idades,
Nota = notas,
HorasEstudo = horas_estudo,
Aprovado = aprovado
)
end
# Criando o DataFrame
df = criar_dados_estudantes()
# Visualizando as primeiras linhas
println("Primeiras linhas do conjunto de dados:")
dfSaída esperada:
Estatísticas Descritivas
Vamos calcular algumas estatísticas descritivas básicas:
# Estatísticas descritivas para colunas numéricas
function resumo_estatistico(df)
println("Estatísticas Descritivas:")
println("------------------------")
for col in names(df)
if eltype(df[!, col]) <: Number
println("\nVariável: ", col)
println(" Média: ", round(mean(skipmissing(df[!, col])), digits=2))
println(" Mediana: ", median(skipmissing(df[!, col])))
println(" Mínimo: ", minimum(skipmissing(df[!, col])))
println(" Máximo: ", maximum(skipmissing(df[!, col])))
println(" Desvio Padrão: ", round(std(skipmissing(df[!, col])), digits=2))
end
end
# Contagem para variáveis categóricas
println("\nContagem por categoria (Aprovado):")
println(combine(groupby(df, :Aprovado), nrow => :Contagem))
end
resumo_estatistico(df)Saída esperada:
Visualização dos Dados
1. Histograma das Notas
# Criando um histograma das notas
histogram(df.Nota,
bins=5,
xlabel="Notas",
ylabel="Frequência",
title="Distribuição das Notas",
color=:steelblue,
alpha=0.6,
lw=0,
legend=false,
xlims=(4, 10),
xticks=4:10)Saída do Histograma:
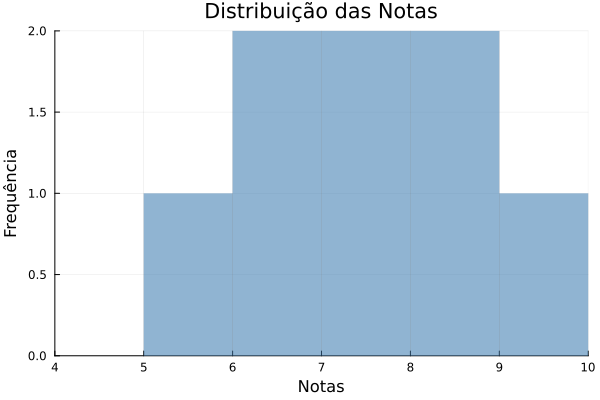
2. Gráfico de Dispersão: Horas de Estudo vs Notas
# Criando um gráfico de dispersão
scatter(df.HorasEstudo, df.Nota,
xlabel="Horas de Estudo",
ylabel="Nota",
title="Relação entre Horas de Estudo e Notas",
color=:blue,
legend=false,
markersize=8,
markercolor=:white,
markerstrokecolor=:steelblue,
markerstrokewidth=2,
xlims=(8, 20),
ylims=(4, 10),
xticks=8:20,
yticks=4:10)
# Adicionando uma linha de tendência
x_range = minimum(df.HorasEstudo):0.1:maximum(df.HorasEstudo)
coef = cov(df.HorasEstudo, df.Nota) / var(df.HorasEstudo)
intercept = mean(df.Nota) - coef * mean(df.HorasEstudo)
plot!(x_range, x -> intercept + coef * x,
linewidth=2,
linestyle=:dash,
color=:darkred,
label="Linha de Tendência")Saída do Gráfico de Dispersão:
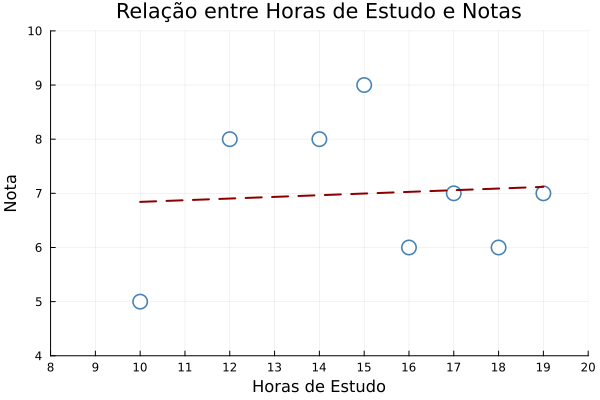
3. Boxplot das Horas de Estudo por Status de Aprovação
using StatsPlots
# Criando um boxplot agrupado por aprovação
boxplot(df.Aprovado, df.HorasEstudo;
xlabel="Aprovado",
ylabel="Horas de Estudo",
title="Distribuição de Horas de Estudo por Status de Aprovação",
color=:steelblue,
legend=false)Saída do Boxplot:
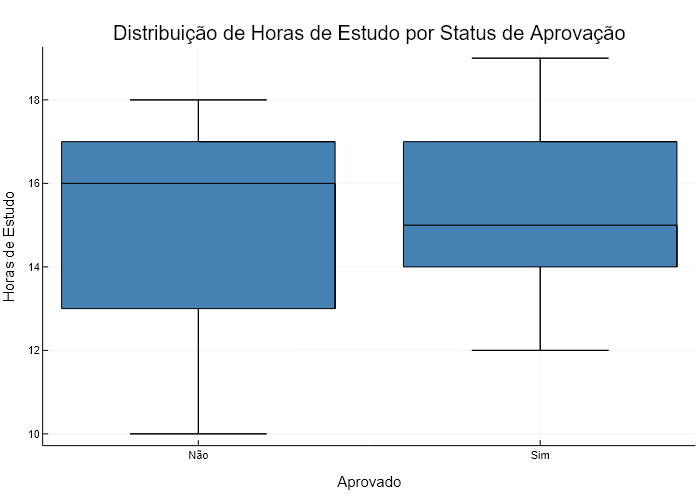
Análise dos Resultados
Com base na análise exploratória, podemos tirar as seguintes conclusões:
- Distribuição das Notas: As notas variam de 5 a 9, com média de 7.0.
- Relação entre Variáveis: Há uma correlação positiva entre horas de estudo e notas, sugerindo que alunos que estudam mais tendem a ter notas melhores.
- Aprovação: 5 dos 8 alunos foram aprovados (nota ≥ 7).
- Idade dos Alunos: A idade média é de aproximadamente 21 anos, variando de 18 a 24 anos.
Próximos Passos
Com base nessa análise exploratória, poderíamos:
- Realizar testes estatísticos para verificar a significância das relações encontradas
- Coletar mais dados para aumentar a confiabilidade das conclusões
- Desenvolver um modelo de classificação para prever a aprovação com base nas outras variáveis
Referências
- Tukey, J. W. (1977). Exploratory Data Analysis. Addison-Wesley.
- Behrens, J. T. (1997). Principles and Procedures of Exploratory Data Analysis. Psychological Methods.
- Wickham, H., & Grolemund, G. (2016). R for Data Science. O’Reilly Media.
