
A análise multivariada é um conjunto de técnicas estatísticas utilizadas para analisar dados que envolvem mais de uma variável ao mesmo tempo. Ela permite compreender relações complexas entre variáveis, identificar padrões ocultos e construir modelos preditivos mais robustos e realistas.
O que é Análise Multivariada?
Diferente da análise univariada (uma variável) ou bivariada (duas variáveis), a análise multivariada considera múltiplas variáveis simultaneamente, permitindo uma visão mais completa e precisa dos fenômenos estudados.
Principais Técnicas
1. Técnicas de Dependência
- Regressão Linear Múltipla: Prediz uma variável dependente usando múltiplas variáveis independentes
- Regressão Logística: Para variáveis dependentes categóricas
- Análise Discriminante: Classifica observações em grupos pré-definidos
- Análise de Correspondência: Examina relações entre variáveis categóricas
2. Técnicas de Interdependência
- Análise de Componentes Principais (PCA): Reduz dimensionalidade preservando informação
- Análise Fatorial: Identifica fatores latentes que explicam correlações
- Análise de Agrupamento (Clusterização): Agrupa observações similares
- Análise de Correspondência Múltipla: Extensão do PCA para dados categóricos
3. Técnicas Avançadas
- Análise de Séries Temporais Multivariadas: Para dados temporais com múltiplas variáveis
- Modelos de Equações Estruturais: Para testar modelos causais complexos
- Análise Canônica: Examina relações entre dois conjuntos de variáveis
Regressão Linear Múltipla - Fundamentos
A regressão linear múltipla é uma extensão natural da regressão linear simples, permitindo modelar a relação entre uma variável resposta e múltiplas variáveis explicativas.
Equação Geral
\[Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_pX_p + \varepsilon\]Onde:
- $Y$: variável dependente (resposta)
- $X_1, X_2, …, X_p$: variáveis independentes (explicativas)
- $\beta_0$: intercepto (valor de Y quando todas as X são zero)
- $\beta_1, \beta_2, …, \beta_p$: coeficientes de regressão
- $\varepsilon$: erro aleatório (resíduos)
Pressupostos Fundamentais
- Linearidade: Relação linear entre variáveis independentes e dependente
- Independência: Observações são independentes entre si
- Homocedasticidade: Variância constante dos resíduos
- Normalidade: Resíduos seguem distribuição normal
- Ausência de Multicolinearidade: Variáveis independentes não são altamente correlacionadas
Exemplo Prático Completo em Julia
Configuração Inicial e Dados
using DataFrames, GLM, Statistics, StatsPlots, LinearAlgebra
using StatsBase, HypothesisTests, Plots
# Dados expandidos: Desempenho acadêmico
dados = DataFrame(
HorasEstudo = [5, 7, 8, 10, 12, 15, 18, 20, 6, 9, 11, 14, 16, 19, 22, 25],
HorasSono = [6, 7, 6, 8, 7, 9, 8, 7, 5, 8, 6, 9, 7, 8, 6, 7],
Motivacao = [7, 8, 6, 9, 8, 9, 9, 10, 5, 7, 8, 9, 8, 9, 7, 8],
Nota = [6.0, 7.0, 7.5, 8.0, 8.5, 9.0, 9.5, 10.0, 5.5, 7.8, 8.2, 8.8, 9.2, 9.6, 8.5, 9.1]
)
# Visualização inicial dos dados
println("Primeiras linhas dos dados:")
println(first(dados, 5))
println("\nEstatísticas descritivas:")
describe(dados)
Análise Exploratória
# Matriz de correlação
cor_matrix = cor(Matrix(dados))
println("Matriz de Correlação:")
println(cor_matrix)
# Gráfico de dispersão entre variáveis
scatter_plot = scatter(dados.HorasEstudo, dados.Nota,
xlabel="Horas de Estudo", ylabel="Nota",
title="Relação: Horas de Estudo vs Nota",
legend=false, alpha=0.7)
display(scatter_plot)
# Histogramas das variáveis
hist_plots = [histogram(dados[!, col], title=string(col), bins=8)
for col in names(dados)]
plot(hist_plots..., layout=(2,2), size=(800,600))
Ajuste e Diagnóstico do Modelo
# Modelo completo
modelo_completo = lm(@formula(Nota ~ HorasEstudo + HorasSono + Motivacao), dados)
# Resumo detalhado
println("=== RESUMO DO MODELO ===")
println(modelo_completo)
println("\n=== COEFICIENTES ===")
println(coeftable(modelo_completo))
# Métricas de qualidade
r2 = r2(modelo_completo)
r2_adj = adjr2(modelo_completo)
println("\nR² = ", round(r2, digits=4))
println("R² Ajustado = ", round(r2_adj, digits=4))
# Resíduos
residuos = residuals(modelo_completo)
valores_preditos = predict(modelo_completo)
# Diagnóstico de resíduos
residuos_plot = scatter(valores_preditos, residuos,
xlabel="Valores Preditos", ylabel="Resíduos",
title="Análise de Resíduos", legend=false)
hline!([0], color=:red, linestyle=:dash)
display(residuos_plot)
# Teste de normalidade dos resíduos
shapiro_test = ShapiroWilkTest(residuos)
println("\nTeste de Shapiro-Wilk para normalidade dos resíduos:")
println("p-valor = ", pvalue(shapiro_test))
Predições e Intervalos de Confiança
# Novos dados para predição
novos_dados = DataFrame(
HorasEstudo = [14, 16, 18],
HorasSono = [8, 7, 9],
Motivacao = [8, 9, 8]
)
# Predições
predicoes = predict(modelo_completo, novos_dados)
println("=== PREDIÇÕES ===")
for i in 1:nrow(novos_dados)
println("Cenário $i: Estudo=$(novos_dados.HorasEstudo[i])h, " *
"Sono=$(novos_dados.HorasSono[i])h, " *
"Motivação=$(novos_dados.Motivacao[i]) → " *
"Nota Prevista: $(round(predicoes[i], digits=2))")
end
# Análise de importância das variáveis
coefs = coef(modelo_completo)[2:end] # Excluir intercepto
nomes_vars = ["HorasEstudo", "HorasSono", "Motivacao"]
importancia = abs.(coefs)
println("\n=== IMPORTÂNCIA DAS VARIÁVEIS ===")
for (nome, imp) in zip(nomes_vars, importancia)
println("$nome: $(round(imp, digits=3))")
end
Interpretação Detalhada dos Resultados
Coeficientes de Regressão
Cada coeficiente $\beta_i$ representa a mudança esperada na variável dependente para um aumento unitário na variável independente correspondente, mantendo todas as outras variáveis constantes (ceteris paribus).
Exemplo de Interpretação:
- Se $\beta_1 = 0.18$ (HorasEstudo): Para cada hora adicional de estudo, a nota aumenta em 0.18 pontos, mantendo sono e motivação constantes.
- Se $\beta_2 = 0.25$ (HorasSono): Para cada hora adicional de sono, a nota aumenta em 0.25 pontos, mantendo estudo e motivação constantes.
Métricas de Qualidade do Modelo
R² (Coeficiente de Determinação)
- Indica a proporção da variância de Y explicada pelo modelo
- Varia entre 0 e 1 (0% a 100%)
- R² = 0.85 significa que 85% da variação nas notas é explicada pelas variáveis do modelo
R² Ajustado
- Ajusta o R² pelo número de variáveis e tamanho da amostra
- Mais apropriado para comparar modelos com diferentes números de variáveis
- Penaliza a inclusão de variáveis irrelevantes
Teste F Global
- Testa se pelo menos uma variável independente é significativa
- H₀: β₁ = β₂ = … = βₚ = 0
- p-valor < 0.05 indica que o modelo é estatisticamente significativo
Técnicas Complementares
Análise de Componentes Principais (PCA)
using MultivariateStats
# Preparar dados para PCA (padronizar)
dados_numericos = select(dados, Not(:Nota))
dados_padronizados = (Matrix(dados_numericos) .- mean(Matrix(dados_numericos), dims=1)) ./
std(Matrix(dados_numericos), dims=1)
# Aplicar PCA
pca_model = fit(PCA, dados_padronizados')
componentes = transform(pca_model, dados_padronizados')
# Variância explicada
var_explicada = principalvars(pca_model)
var_prop = var_explicada ./ sum(var_explicada)
println("=== ANÁLISE PCA ===")
println("Variância explicada por componente:")
for i in 1:length(var_prop)
println("PC$i: $(round(var_prop[i]*100, digits=1))%")
end
# Biplot conceitual
scatter(componentes[1,:], componentes[2,:],
xlabel="PC1 ($(round(var_prop[1]*100, digits=1))%)",
ylabel="PC2 ($(round(var_prop[2]*100, digits=1))%)",
title="PCA - Primeiros Dois Componentes")
O que é PCA (Análise de Componentes Principais)?
A Análise de Componentes Principais (PCA) é uma técnica de redução de dimensionalidade que transforma um conjunto de variáveis possivelmente correlacionadas em um conjunto menor de variáveis não correlacionadas chamadas componentes principais.
Formulação Matemática
Seja X uma matriz de dados $n \times p$, onde:
- $n$ = número de observações
- $p$ = número de variáveis
Passo 1: Padronização
Os dados são padronizados para ter média zero e variância unitária:
\[\mathbf{Z} = \frac{\mathbf{X} - \boldsymbol{\mu}}{\boldsymbol{\sigma}}\]onde $\boldsymbol{\mu}$ é o vetor de médias e $\boldsymbol{\sigma}$ é o vetor de desvios-padrão.
Passo 2: Matriz de Covariância
A matriz de covariância dos dados padronizados é:
\[\mathbf{C} = \frac{1}{n-1}\mathbf{Z}^T\mathbf{Z}\]Passo 3: Decomposição Espectral
Os componentes principais são obtidos através da decomposição espectral de C:
\[\mathbf{C} = \mathbf{V}\mathbf{\Lambda}\mathbf{V}^T\]onde:
- $\mathbf{V}$ = matriz dos autovetores (loadings)
- $\mathbf{\Lambda}$ = matriz diagonal dos autovalores
Passo 4: Transformação dos Dados
Os scores (coordenadas dos pontos no novo espaço) são calculados como:
\[\mathbf{Y} = \mathbf{Z}\mathbf{V}\]O que é um Biplot?
Um biplot é uma representação gráfica que mostra simultaneamente:
- Observações (pontos) projetadas no espaço dos componentes principais
- Variáveis originais (setas) representadas pelos seus loadings
Componentes do Biplot
1. Pontos (Scores)
Cada ponto representa uma observação no espaço bidimensional PC1-PC2:
\[\text{Ponto}_i = (y_{i1}, y_{i2})\]onde $y_{ij}$ é o score da observação $i$ no componente principal $j$.
2. Setas (Loadings)
Cada seta representa uma variável original e mostra:
\[\text{Seta}_k = (v_{k1}, v_{k2})\]onde $v_{kj}$ é o loading da variável $k$ no componente principal $j$.
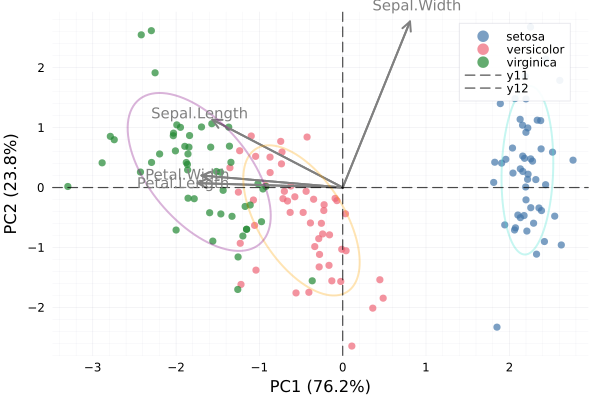
Interpretação do Biplot do Dataset Iris
Informações do Gráfico
Eixos:
- PC1: Primeiro componente principal (maior variância explicada)
- PC2: Segundo componente principal (segunda maior variância)
Porcentagem de Variância Explicada:
- PC1 ≈ 73%
- PC2 ≈ 23%
- Total ≈ 96% da variância original é preservada
Interpretação das Setas (Variáveis)
As quatro setas representam as medidas das flores:
- Sepal.Length (Comprimento da Sépala)
- Sepal.Width (Largura da Sépala)
- Petal.Length (Comprimento da Pétala)
- Petal.Width (Largura da Pétala)
Propriedades das Setas:
Comprimento:
- Setas mais longas = variáveis com maior contribuição para os componentes principais
- Setas mais curtas = variáveis com menor contribuição
Direção:
- Setas apontando na mesma direção = variáveis positivamente correlacionadas
- Setas apontando em direções opostas = variáveis negativamente correlacionadas
- Setas perpendiculares = variáveis não correlacionadas
Ângulo com os eixos:
- Seta paralela ao PC1 = variável contribui principalmente para PC1
- Seta paralela ao PC2 = variável contribui principalmente para PC2
Interpretação dos Pontos (Observações)
Cores dos Pontos:
- Azul: Iris setosa
- Laranja: Iris versicolor
- Verde: Iris virginica
Posicionamento:
- Pontos próximos = observações similares
- Pontos distantes = observações diferentes
Elipses de Confiança
As elipses coloridas representam regiões de confiança estatística (≈68%) para cada espécie:
\[\text{Elipse} = \{(\mathbf{x} - \boldsymbol{\mu})^T\mathbf{C}^{-1}(\mathbf{x} - \boldsymbol{\mu}) \leq \chi^2_{2,0.68}\}\]onde:
- $\boldsymbol{\mu}$ = centroide do grupo
- $\mathbf{C}$ = matriz de covariância do grupo
- $\chi^2_{2,0.68}$ = quantil da distribuição qui-quadrado
Conclusões do Biplot Iris
Padrões Observados:
- Separação Clara: As três espécies formam grupos bem distintos
- Setosa vs. Outras: Iris setosa está claramente separada das outras duas espécies
- Correlações:
- Comprimento e largura da pétala são altamente correlacionados
- Largura da sépala tem comportamento diferente das outras medidas
Interpretação Biológica:
- PC1 parece representar o “tamanho geral” da flor (todas as medidas exceto largura da sépala)
- PC2 está relacionado principalmente com a largura da sépala
- Iris setosa tem características distintas (menor tamanho geral, maior largura relativa da sépala)
- Iris versicolor e virginica são mais similares entre si, mas ainda distinguíveis
Vantagens do Biplot:
- Redução de Dimensionalidade: 4 variáveis → 2 dimensões (96% da variância preservada)
- Visualização Completa: Mostra relações entre variáveis E observações simultaneamente
- Interpretabilidade: Permite entender tanto a estrutura dos dados quanto as relações entre variáveis
- Identificação de Padrões: Facilita a identificação de grupos e outliers
O biplot é uma ferramenta poderosa que combina a análise exploratória de dados com rigor estatístico, fornecendo insights tanto sobre a estrutura dos dados quanto sobre as relações entre as variáveis originais.
Exemplo Prático Completo em Julia
# PCA Biplot para o Dataset Iris em Julia
using RDatasets, MultivariateStats, Plots, StatsBase, Statistics, Distributions, LinearAlgebra
# Carregar o dataset Iris
iris = dataset("datasets", "iris")
# Preparar os dados (apenas as variáveis numéricas)
X = Matrix(iris[:, 1:4])' # Transpor para ter variáveis nas linhas
species = iris.Species
# Padronizar os dados (centrar e escalar)
X_std = standardize(ZScoreTransform, X, dims=2)
# Realizar PCA
pca_model = fit(PCA, X_std; maxoutdim=2)
# Obter as coordenadas dos pontos (scores)
scores = predict(pca_model, X_std)'
# Obter os loadings (coeficientes das variáveis) - apenas PC1 e PC2
loadings = projection(pca_model) # Não transpor ainda
loadings_2d = loadings[:, 1:2] # Pegar apenas as 2 primeiras colunas
# Nomes das variáveis
var_names = ["Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width"]
# Criar o biplot
p = scatter(scores[:, 1], scores[:, 2],
group=species,
xlabel="PC1 ($(round(principalvars(pca_model)[1]/sum(principalvars(pca_model))*100, digits=1))%)",
ylabel="PC2 ($(round(principalvars(pca_model)[2]/sum(principalvars(pca_model))*100, digits=1))%)",
title="",
legend=:topright,
alpha=0.7,
markersize=4)
# Adicionar as setas dos loadings (multiplicar por fator para visualização)
scale_factor = 3.0
for i in 1:4
quiver!(p, [0], [0],
quiver=([loadings_2d[i, 1] * scale_factor], [loadings_2d[i, 2] * scale_factor]),
color=:grey, linewidth=2, arrow=true)
# Adicionar labels das variáveis
annotate!(p, loadings_2d[i, 1] * scale_factor * 1.1,
loadings_2d[i, 2] * scale_factor * 1.1,
text(var_names[i], 10, :grey))
end
# Função para criar elipse de confiança
function confidence_ellipse(x, y, confidence=0.95)
n = length(x)
if n < 3
return x, y # Não é possível criar elipse com menos de 3 pontos
end
# Calcular centro
cx = mean(x)
cy = mean(y)
# Calcular matriz de covariância
cov_matrix = cov([x y])
# Eigendecomposition
eigenvals, eigenvecs = eigen(cov_matrix)
# Fator de escala baseado na distribuição chi-quadrado
scale = sqrt(quantile(Chisq(2), confidence))
# Criar pontos da elipse
theta = range(0, 2π, length=100)
ellipse_x = zeros(100)
ellipse_y = zeros(100)
for i in 1:100
point = [cos(theta[i]), sin(theta[i])]
scaled_point = scale * sqrt.(eigenvals) .* point
rotated_point = eigenvecs * scaled_point
ellipse_x[i] = cx + rotated_point[1]
ellipse_y[i] = cy + rotated_point[2]
end
return ellipse_x, ellipse_y
end
# Adicionar elipses de confiança para cada espécie
species_unique = unique(species)
colors = [:turquoise, :orange, :purple] # Cores correspondentes aos grupos
for (i, sp) in enumerate(species_unique)
mask = species .== sp
x_group = scores[mask, 1]
y_group = scores[mask, 2]
if length(x_group) > 2 # Precisa de pelo menos 3 pontos
ellipse_x, ellipse_y = confidence_ellipse(x_group, y_group, 0.68) # ~1 desvio padrão
plot!(p, ellipse_x, ellipse_y,
linewidth=2,
linestyle=:solid,
color=colors[i],
alpha=0.3,
fillalpha=0.1,
fillcolor=colors[i],
label="")
end
end
# Adicionar linhas de referência
hline!(p, [0], color=:black, linestyle=:dash, alpha=0.7)
vline!(p, [0], color=:black, linestyle=:dash, alpha=0.7)
# Mostrar o gráfico
display(p)
# Imprimir informações adicionais
println("Variância explicada:")
println("PC1: $(round(principalvars(pca_model)[1]/sum(principalvars(pca_model))*100, digits=2))%")
println("PC2: $(round(principalvars(pca_model)[2]/sum(principalvars(pca_model))*100, digits=2))%")
println("Total: $(round(sum(principalvars(pca_model)[1:2])/sum(principalvars(pca_model))*100, digits=2))%")
println("\nLoadings (Componentes Principais):")
println("Variável\t\tPC1\t\tPC2")
for i in 1:4
println("$(var_names[i])\t$(round(loadings_2d[i,1], digits=3))\t\t$(round(loadings_2d[i,2], digits=3))")
end
Análise de Agrupamento (K-means)
using Clustering
# Aplicar K-means com 3 clusters
kmeans_result = kmeans(dados_padronizados', 3)
clusters = assignments(kmeans_result)
# Adicionar clusters aos dados originais
dados_com_clusters = copy(dados)
dados_com_clusters.Cluster = clusters
println("=== ANÁLISE DE CLUSTERS ===")
println("Distribuição dos clusters:")
println(countmap(clusters))
# Visualizar clusters
scatter(dados.HorasEstudo, dados.Nota,
group=clusters,
xlabel="Horas de Estudo", ylabel="Nota",
title="Clusters Identificados")
Dados de Exemplo Expandidos
| Horas Estudo | Horas Sono | Motivação (1-10) | Nota |
|---|---|---|---|
| 5 | 6 | 7 | 6.0 |
| 7 | 7 | 8 | 7.0 |
| 8 | 6 | 6 | 7.5 |
| 10 | 8 | 9 | 8.0 |
| 12 | 7 | 8 | 8.5 |
| 15 | 9 | 9 | 9.0 |
| 18 | 8 | 9 | 9.5 |
| 20 | 7 | 10 | 10.0 |
Problemas Comuns e Soluções
1. Multicolinearidade
Problema: Variáveis independentes altamente correlacionadas Detecção: VIF (Variance Inflation Factor) > 10 Soluções:
- Remover variáveis redundantes
- Usar técnicas de regularização (Ridge, Lasso)
- Aplicar PCA antes da regressão
2. Heterocedasticidade
Problema: Variância dos resíduos não constante Detecção: Gráfico de resíduos vs valores preditos Soluções:
- Transformação de variáveis (log, raiz quadrada)
- Modelos com heterocedasticidade robusta
- Regressão ponderada
3. Não-linearidade
Problema: Relação não-linear entre variáveis Detecção: Padrões nos gráficos de resíduos Soluções:
- Incluir termos quadráticos/cúbicos
- Transformação de variáveis
- Modelos não-lineares
4. Outliers e Pontos Influentes
Problema: Observações que afetam drasticamente o modelo Detecção: Distância de Cook, resíduos padronizados Soluções:
- Investigar a natureza dos outliers
- Modelos robustos
- Transformação de dados
Aplicações Práticas
1. Marketing e Vendas
- Análise de fatores que influenciam vendas
- Segmentação de clientes
- Otimização de campanhas publicitárias
2. Medicina e Saúde
- Identificação de fatores de risco
- Desenvolvimento de escores prognósticos
- Análise de eficácia de tratamentos
3. Finanças
- Modelos de precificação de ativos
- Análise de risco de crédito
- Portfolio optimization
4. Engenharia e Qualidade
- Controle de qualidade multivariado
- Otimização de processos
- Análise de confiabilidade
5. Ciências Sociais
- Análise de fatores socioeconômicos
- Pesquisas de opinião pública
- Estudos comportamentais
Quando Usar Análise Multivariada?
Critérios de Aplicação:
-
Múltiplas Variáveis Relevantes: Quando o fenômeno é influenciado por diversos fatores simultaneamente
-
Controle de Confundimento: Para isolar o efeito de uma variável controlando outras
-
Melhoria da Precisão: Quando modelos univariados são insuficientes
-
Exploração de Padrões: Para descobrir estruturas ocultas em dados complexos
-
Predição Robusta: Quando se necessita de modelos preditivos mais confiáveis
Vantagens:
- Modelos mais realistas e completos
- Controle de variáveis confundidoras
- Maior poder explicativo
- Melhor capacidade preditiva
- Insights mais profundos sobre relações complexas
Limitações:
- Maior complexidade interpretativa
- Necessita amostras maiores
- Pressupostos mais restritivos
- Risco de overfitting
- Possibilidade de multicolinearidade
Conclusão
A análise multivariada representa uma evolução natural das técnicas estatísticas clássicas, permitindo uma compreensão mais completa e nuançada dos fenômenos complexos que caracterizam o mundo real. Sua aplicação adequada requer não apenas conhecimento técnico, mas também uma compreensão profunda do contexto dos dados e dos objetivos da análise.
O domínio dessas técnicas é fundamental para profissionais de ciência de dados, pesquisadores e analistas que buscam extrair insights significativos de conjuntos de dados multidimensionais, contribuindo para tomadas de decisão mais informadas e estratégias mais eficazes em suas respectivas áreas de atuação.
A escolha da técnica apropriada deve sempre considerar a natureza dos dados, os objetivos da análise, o tamanho da amostra e os pressupostos metodológicos, garantindo que os resultados sejam não apenas estatisticamente válidos, mas também praticamente relevantes.
