Teorema do Limite Central

O Teorema do Limite Central (TLC) é um dos resultados mais importantes da teoria da probabilidade. Ele estabelece que a soma (ou média) de um grande número de variáveis aleatórias independentes e identicamente distribuídas tende a seguir uma distribuição normal.

📊 Importante: O TLC é fundamental para a inferência estatística.
Ele justifica o uso da distribuição normal em muitas aplicações práticas e é a base para a construção de intervalos de confiança e testes de hipóteses.

1. Contexto Histórico

O Teorema do Limite Central tem uma rica história que se estende por mais de dois séculos:

1.1 Desenvolvimento Histórico

Abraham de Moivre (1733): Primeira versão do teorema, aplicada à distribuição binomial
Pierre-Simon Laplace (1812): Generalização para outras distribuições
Aleksandr Lyapunov (1901): Prova rigorosa e condições necessárias
Paul Lévy (1935): Formulação moderna e extensões

1.2 Importância Histórica

O TLC revolucionou a estatística ao:

Justificar o uso da distribuição normal em análises estatísticas
Permitir a aproximação de distribuições complexas
Fundamentar métodos de inferência estatística

2. Enunciado Formal

Sejam X₁, X₂, …, Xₙ variáveis aleatórias independentes e identicamente distribuídas com:

Média: μ
Variância: σ²

Então, para n suficientemente grande:

\[\frac{\sum_{i=1}^n X_i - n\mu}{\sigma\sqrt{n}} \xrightarrow{d} N(0,1)\]

Ou, equivalentemente, para a média amostral:

\[\frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \xrightarrow{d} N(0,1)\]

onde $\xrightarrow{d}$ indica convergência em distribuição.

3. Demonstração Visual com Julia

Vamos demonstrar o TLC através de simulações com diferentes distribuições:

julia

using Distributions, Plots, Random
using StatsPlots
using Measures

Random.seed!(123)

# Parâmetros
n_amostras = 1000
tamanho_amostra = 30

# Distribuições
dist_unif = Uniform(0, 1)
dist_exp = Exponential(1)
dist_bin = Binomial(1, 0.5)

# Geração das médias amostrais
medias_unif = [mean(rand(dist_unif, tamanho_amostra)) for _ in 1:n_amostras]
medias_exp = [mean(rand(dist_exp, tamanho_amostra)) for _ in 1:n_amostras]
medias_bin = [mean(rand(dist_bin, tamanho_amostra)) for _ in 1:n_amostras]

# Padronização
padronizar(x) = (x .- mean(x)) ./ std(x)
medias_unif_pad = padronizar(medias_unif)
medias_exp_pad = padronizar(medias_exp)
medias_bin_pad = padronizar(medias_bin)

# Curva normal
x = range(-4, 4, length=200)
dist_normal = Normal(0, 1)
curva_normal = pdf.(dist_normal, x)

# Cores distintas
cores = [:darkorange, :seagreen, :royalblue]

# Histogramas
p1 = histogram(medias_unif_pad,
    normalize=:pdf, bins=30,
    title="Médias Amostrais\n(Distribuição Uniforme)",
    xlabel="Valor Padronizado", ylabel="Densidade",
    label="Médias Amostrais",
    color=cores[1], alpha=0.6, linealpha=0,
    bottom_margin=5mm, top_margin=10mm)

plot!(p1, x, curva_normal, label="Normal(0,1)", color=:black, lw=2, linestyle=:dash)

p2 = histogram(medias_exp_pad,
    normalize=:pdf, bins=30,
    title="Médias Amostrais\n(Distribuição Exponencial)",
    xlabel="Valor Padronizado", ylabel="Densidade",
    label="Médias Amostrais",
    color=cores[2], alpha=0.6, linealpha=0,
    bottom_margin=5mm, top_margin=10mm)

plot!(p2, x, curva_normal, label="Normal(0,1)", color=:black, lw=2, linestyle=:dash)

p3 = histogram(medias_bin_pad,
    normalize=:pdf, bins=30,
    title="Médias Amostrais\n(Distribuição Binomial)",
    xlabel="Valor Padronizado", ylabel="Densidade",
    label="Médias Amostrais",
    color=cores[3], alpha=0.6, linealpha=0,
    bottom_margin=5mm, top_margin=10mm)

plot!(p3, x, curva_normal, label="Normal(0,1)", color=:black, lw=2, linestyle=:dash)


# Plot final com margens ajustadas para evitar corte
plot(p1, p2, p3,
    layout=(1,3),
    size=(1350, 450),
    titlefontsize=14,
    layout_margin=10mm,
    left_margin=10mm,
    right_margin=10mm,
    top_margin=15mm,
    bottom_margin=10mm,
    legend=:topright,
    grid=true)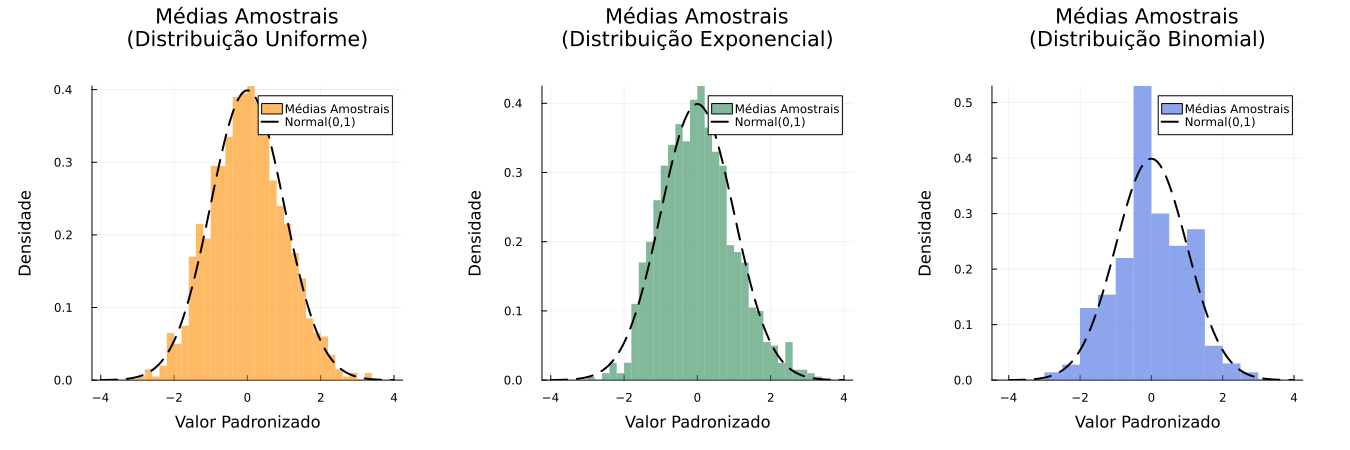

Demonstração do TLC

Figura 1: Demonstração do Teorema do Limite Central para diferentes distribuições (Uniforme, Exponencial e Binomial)

4. Condições e Considerações

4.1 Requisitos Fundamentais

Variáveis aleatórias independentes
Identicamente distribuídas
Variância finita
n “suficientemente grande” (geralmente n ≥ 30)

4.2 Velocidade de Convergência

A velocidade de convergência para a normalidade depende de vários fatores:

Assimetria da distribuição original
Curtose (peso das caudas)
Tamanho da amostra

Vamos analisar como o tamanho da amostra afeta a convergência:

julia

using Distributions, Plots, Random

# Configurações
Random.seed!(123)
n_amostras = 1000
tamanhos = [2, 5, 10, 30]

# Distribuição exponencial (assimétrica)
dist = Exponential(1)

# Função para gerar médias amostrais
function gerar_medias(dist, n, tamanho)
    return [mean(rand(dist, tamanho)) for _ in 1:n]
end

# Gerando médias para diferentes tamanhos de amostra
medias = [gerar_medias(dist, n_amostras, t) for t in tamanhos]
medias_pad = [padronizar(m) for m in medias]

# Criando os QQ-plots
plots = []
for (i, t) in enumerate(tamanhos)
    p = qqplot(Normal(0,1), medias_pad[i],
        qqline=:R,
        title="n = $t",
        label="",
        markercolor=:steelblue,
        markeralpha=0.6,
        linecolor=:red)
    push!(plots, p)
end

# Combinando os plots
plot(plots..., 
    layout=(2,2), 
    size=(800,800),
    title="Convergência do TLC",
    titlefontsize=12)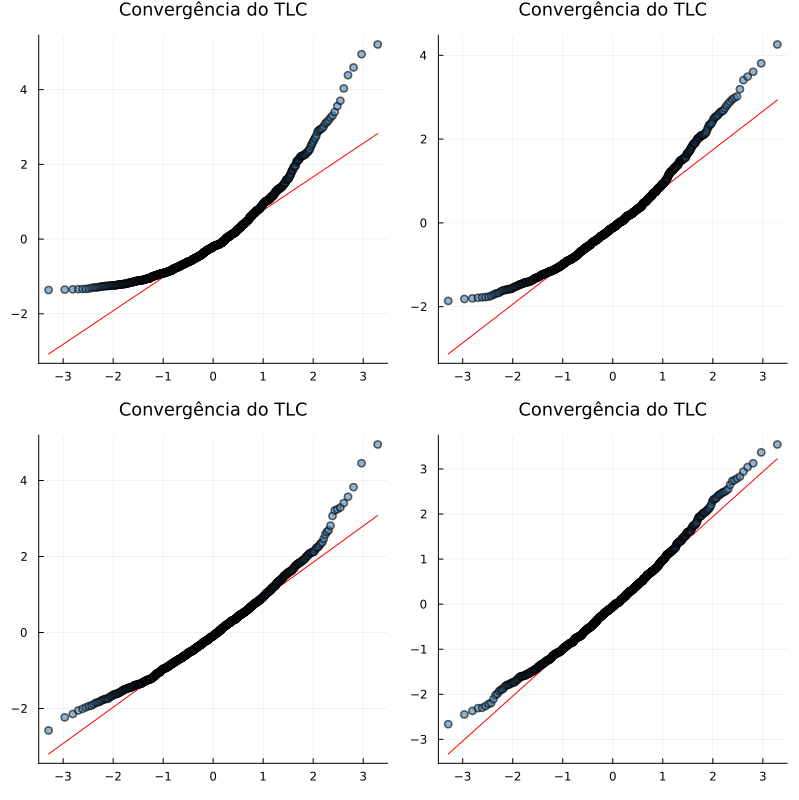

Convergência do TLC

Figura 2: Análise da convergência do TLC para diferentes tamanhos de amostra

5. Aplicações Práticas

5.1 Intervalos de Confiança

Para uma amostra grande (n ≥ 30), o intervalo de confiança de 95% para a média é:

\[\bar{X} \pm 1.96 \frac{\sigma}{\sqrt{n}}\]

5.2 Teste de Hipóteses

A estatística Z para teste de hipóteses:

\[Z = \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}\]

5.3 Exemplo Prático: Controle de Qualidade

Considere uma fábrica que produz parafusos. O comprimento dos parafusos deve ser 10mm ± 0.1mm.

julia

using Distributions, Statistics

# Simulando medições de parafusos
n = 100  # tamanho da amostra
μ = 10.0  # média desejada
σ = 0.02  # desvio padrão do processo

# Gerando medições
medidas = rand(Normal(μ, σ), n)

# Calculando estatísticas
x̄ = mean(medidas)
erro_padrao = std(medidas)/√n

# Intervalo de confiança de 95%
z = 1.96
ic_inferior = x̄ - z * erro_padrao
ic_superior = x̄ + z * erro_padrao

println("Média das medidas: ", round(x̄, digits=4), " mm")
println("Intervalo de confiança 95%: [", 
    round(ic_inferior, digits=4), ", ",
    round(ic_superior, digits=4), "] mm")

Resolução Manual Passo a Passo

Vamos resolver manualmente o exemplo acima para entender melhor o processo.

Dados do problema:

Tamanho da amostra: $n = 100$ parafusos
Média desejada: $\mu = 10.0$ mm
Desvio padrão do processo: $\sigma = 0.02$ mm
Nível de confiança: 95% $\rightarrow z_{\alpha/2} = 1.96$

Passo 1: Calcular o Erro Padrão

O erro padrão (EP) é dado pela fórmula:

\[EP = \frac{\sigma}{\sqrt{n}}\]

Substituindo os valores:

\[EP = \frac{0.02}{\sqrt{100}} = \frac{0.02}{10} = 0.002 \text{ mm}\]

Passo 2: Calcular o Intervalo de Confiança

Para um intervalo de confiança de 95%, utilizamos a fórmula:

\[IC_{95\%} = \bar{x} \pm z_{\alpha/2} \cdot EP\]

Onde:

$\bar{x}$ é a média amostral (supondo $\bar{x} = 10.002$ mm)
$z_{\alpha/2} = 1.96$ para 95% de confiança

Substituindo os valores:

\[IC_{95\%} = 10.002 \pm 1.96 \cdot 0.002\]

Limite inferior: $IC_{inferior} = 10.002 - (1.96 \cdot 0.002) = 10.002 - 0.00392 = 9.99808 \text{ mm}$

Limite superior: $IC_{superior} = 10.002 + (1.96 \cdot 0.002) = 10.002 + 0.00392 = 10.00592 \text{ mm}$

Portanto:

\[IC_{95\%} = [9.99808, 10.00592] \text{ mm}\]

Interpretação dos Resultados:

A média amostral é $\bar{x} = 10.002 \text{ mm}$
Com 95% de confiança, o intervalo $[9.99808, 10.00592]$ contém a verdadeira média populacional $\mu$
Como o intervalo de tolerância especificado é $10 \pm 0.1 \text{ mm}$ (ou seja, $[9.9, 10.1] \text{ mm}$), e $IC_{95\%} \subset [9.9, 10.1]$, podemos concluir que o processo está sob controle estatístico

Conclusão: O processo de fabricação está produzindo parafusos dentro das especificações requeridas $(10 \pm 0.1 \text{ mm})$ com 95% de confiança. A variabilidade do processo é pequena, como evidenciado pelo intervalo de confiança estreito (aproximadamente $\pm 0.004 \text{ mm}$ ao redor da média).

5.4 Aplicações em Diferentes Áreas

Finanças
- Análise de retornos de investimentos
- Cálculo de Value at Risk (VaR)
- Precificação de opções
Medicina
- Análise de ensaios clínicos
- Estudos epidemiológicos
- Testes de eficácia de medicamentos
Engenharia
- Controle de qualidade
- Análise de confiabilidade
- Tolerância de fabricação
Ciências Sociais
- Pesquisas de opinião
- Estudos demográficos
- Análise de comportamento

6. Extensões e Variações

6.1 Teorema do Limite Central Multivariado

Para vetores aleatórios, onde a convergência é para uma distribuição normal multivariada:

\[\sqrt{n}(\bar{X}_n - \mu) \xrightarrow{d} N_p(0, \Sigma)\]

6.2 Teorema de Berry-Esseen

Fornece uma taxa de convergência para o TLC:

\[\sup_{x} |F_n(x) - \Phi(x)| \leq \frac{C\rho}{\sigma^3\sqrt{n}}\]

onde:

$F_n$ é a função de distribuição acumulada da soma normalizada
$\Phi$ é a função de distribuição normal padrão
$\rho$ é o terceiro momento absoluto
$C$ é uma constante universal

7. Limitações e Considerações

⚠️ Atenção:
O TLC pode não funcionar bem quando:

A amostra é pequena (n < 30)
A distribuição original é muito assimétrica
As variáveis não são independentes
A variância é infinita ou não existe
Há presença de outliers significativos
A distribuição tem caudas pesadas

7.1 Casos Especiais

Distribuições Estáveis: Algumas distribuições não-normais são estáveis sob soma
Distribuições de Cauda Pesada: Podem requerer tamanhos de amostra muito grandes
Dependência: Correlação entre variáveis pode afetar a convergência

8. Dicas para Aplicação Prática

Verificação da Normalidade
- Use QQ-plots
- Teste de Shapiro-Wilk
- Análise de assimetria e curtose
Tamanho da Amostra
- n ≥ 30 é uma regra geral
- Amostras maiores para distribuições mais complexas
- Considere a potência do teste desejada
Diagnóstico
- Examine outliers
- Verifique independência
- Avalie homogeneidade

Referências

Rice, J. A. Mathematical Statistics and Data Analysis. 3ª ed. Duxbury Press, 2006.
Wasserman, L. All of Statistics: A Concise Course in Statistical Inference. Springer, 2004.
DeGroot, M. H.; Schervish, M. J. Probability and Statistics. 4ª ed. Pearson, 2011.
Casella, G.; Berger, R. L. Statistical Inference. 2ª ed. Duxbury, 2001.
Morettin, P. A.; Bussab, W. O. Estatística Básica. 9ª ed. Saraiva, 2017.
Fischer, H. A History of the Central Limit Theorem: From Classical to Modern Probability Theory. Springer, 2011.
Billingsley, P. Probability and Measure. 3ª ed. Wiley, 1995.
Feller, W. An Introduction to Probability Theory and Its Applications. Vol. 2, 2ª ed. Wiley, 1971.

Morrison Külsenn

Estatística Pura

Teorema do Limite Central

1. Contexto Histórico

1.1 Desenvolvimento Histórico

1.2 Importância Histórica

2. Enunciado Formal

3. Demonstração Visual com Julia

4. Condições e Considerações

4.1 Requisitos Fundamentais

4.2 Velocidade de Convergência

5. Aplicações Práticas

5.1 Intervalos de Confiança

5.2 Teste de Hipóteses

5.3 Exemplo Prático: Controle de Qualidade

Resolução Manual Passo a Passo

5.4 Aplicações em Diferentes Áreas

6. Extensões e Variações

6.1 Teorema do Limite Central Multivariado

6.2 Teorema de Berry-Esseen

7. Limitações e Considerações

7.1 Casos Especiais

8. Dicas para Aplicação Prática

Referências

Morrison Külsenn

Estatística Pura

Siga-nos