Standard normal table/Z Table
logo

Morrison Külsenn

Estatística Pura
Siga-nos

Distribuições de Probabilidade

As distribuições de probabilidade são funções matemáticas que descrevem a probabilidade de diferentes resultados para uma variável aleatória. Elas são fundamentais na estatística e na ciência de dados, permitindo modelar e entender fenômenos aleatórios em diversas áreas do conhecimento.

📊 Importante: Escolher a distribuição adequada é essencial para a análise estatística correta.
Cada distribuição tem pressupostos e aplicações específicas que devem ser considerados.

Símbolos e Conceitos Fundamentais

Variáveis Aleatórias

Funções de Probabilidade

1. Distribuições Discretas

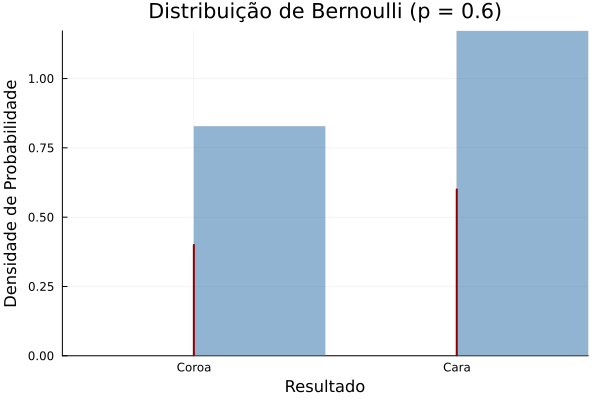
1.1 Distribuição de Bernoulli

Modela experimentos com apenas dois resultados possíveis (sucesso ou fracasso).

Parâmetros

Função de Probabilidade

\(P(X = x) = p^x(1-p)^{1-x}, \text{ onde } x \in \{0,1\}\)

Média e Variância

Aplicações

💡 Exemplo Prático
Lançamento de uma moeda viciada onde a probabilidade de cara (sucesso) é $p=0.6$.
julia
using Distributions, Plots

d = Bernoulli(0.6)
data = rand(d, 1000)

histogram(data, bins=2, normalize=:pdf, 
          legend=false,
          title="Distribuição de Bernoulli (p = 0.6)",
          xlabel="Resultado", 
          ylabel="Densidade de Probabilidade",
          xticks=([0, 1], ["Coroa", "Cara"]),
          color=:steelblue,
          alpha=0.6,
          lw=0,
          xlims=(-0.5, 1.5))

# Linha teórica
plot!([0, 1], [1 - 0.6, 0.6], seriestype=:sticks, color=:darkred, lw=2, label="Teórico")

Distribuição de Bernoulli

Figura 1: Distribuição de Bernoulli para p=0.6

1.2 Distribuição Binomial

Modela o número de sucessos em $n$ tentativas independentes de Bernoulli.

Parâmetros

Função de Probabilidade

\(P(X = k) = C(n,k) \cdot p^k (1-p)^{n-k}, \text{ para } k = 0,1,2,...,n\)

onde $C(n,k) = \frac{n!}{k!(n-k)!}$ é o coeficiente binomial.

Média e Variância

Aplicações

💡 Exemplo Prático
Número de caras em 10 lançamentos de uma moeda justa.
julia
using Distributions, Plots

# Parâmetros da distribuição binomial
n, p = 10, 0.5
d_bin = Binomial(n, p)

x = 0:n
probs_bin = pdf.(d_bin, x)

# Plotando a distribuição binomial (gráfico de barras)
bar(x, probs_bin,
    legend=false,
title="Distribuição Binomial\nAproximação Normal (n = 10, p = 0.5)",
    xlabel="Número de sucessos",
    ylabel="Probabilidade",
    color=:steelblue,
    alpha=0.6,
    lw=0,
    bar_width=0.8,
    ylims=(0, maximum(probs_bin) + 0.05))

# Anotações com valores de probabilidade
annotate!([(x[i], probs_bin[i] + 0.01, text(string(round(probs_bin[i], digits=3)), :black, 8)) for i in 1:length(x)]...)

# Parâmetros da normal aproximada
μ = n * p
σ = sqrt(n * p * (1 - p))
d_normal = Normal(μ, σ)

# Curva da normal: aplicamos a correção de continuidade para melhorar a aproximação
x_dense = range(0, n, length=200)
pdf_normal = pdf.(d_normal, x_dense)

# Sobrepondo a curva normal
plot!(x_dense, pdf_normal, 
      lw=2, color=:darkred, 
      label="Aproximação Normal")

Aproximação Normal da Binomial

Figura 2: Distribuição Binomial com aproximação normal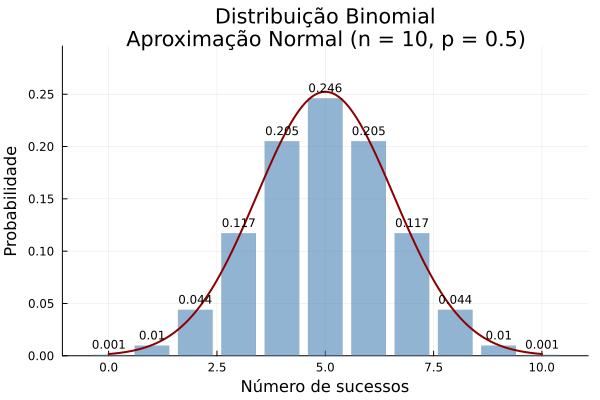

1.3 Distribuição de Poisson

Usada para modelar o número de eventos que ocorrem em um intervalo fixo de tempo ou espaço.

Parâmetro

Função de Probabilidade

\(P(X = k) = \frac{e^{-\lambda} \lambda^k}{k!}, \text{ para } k = 0,1,2,...\)

Média e Variância

Aplicações

💡 Exemplo Prático
Número de chamadas recebidas por um call center em uma hora (λ = 5).
julia
using Distributions, Plots

# Parameter λ (mean rate of occurrences)
λ = 5

# Create Poisson distribution
d = Poisson(λ)

# Values to plot (extending slightly beyond likely range)
x = 0:14
probs = pdf.(d, x)

# Create bar plot
bar(x, probs,
    legend=:topright,
    title="Distribuição de Poisson (λ = $λ)",
    xlabel="Número de Eventos (k)",
    ylabel="Probabilidade P(X = k)",
    color=:steelblue,
    alpha=0.6,
    bar_width=0.8,
    lw=0,
    xticks=x,
    grid=false,
    framestyle=:box)

# Add vertical lines for mean and standard deviation
μ = mean(d)  # For Poisson, μ = λ
σ = std(d)   # For Poisson, σ = √λ
vline!([μ], linestyle=:dash, color=:darkred, linewidth=2, label="Média (μ = $μ)")
vline!([μ - σ, μ + σ], linestyle=:dot, color=:slateblue, linewidth=2, label="±1σ (σ = $(round(σ, digits=2)))")

# Annotate probabilities for significant bars
for (xi, prob) in zip(x, probs)
    if prob > 0.01  # Only label probabilities > 1%
        annotate!(xi, prob + 0.005, text("$(round(prob, digits=3))", 8, :black, :center))
    end
end

# Adjust plot limits
ylims!(0, maximum(probs) + 0.03)
xlims!(-0.5, 14.5)

# Add Poisson PMF formula to plot
annotate!(10, maximum(probs)*0.9, text("Fórmula:\nP(X=k) = e^{-λ}λ^k/k!", 10, :black, :right))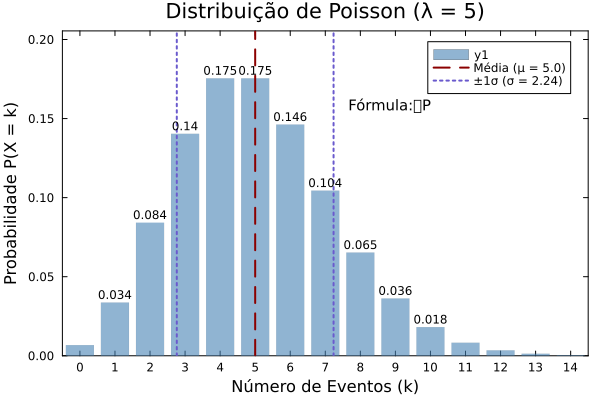

Distribuição de Poisson

Figura 6: Distribuição de Poisson com λ=5
🔍 Curiosidade Histórica
A distribuição de Poisson foi introduzida por Siméon Denis Poisson em 1837 em seu trabalho sobre a probabilidade de condenações em julgamentos criminais.

2. Distribuições Contínuas

2.1 Distribuição Normal (Gaussiana)

A distribuição mais importante em estatística, com forma de sino simétrico.

Parâmetros

Função Densidade de Probabilidade

\(f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)

Propriedades

Aplicações

💡 Exemplo Prático
Distribuição de alturas de uma população (μ = 170cm, σ = 10cm).
julia
using Distributions, Plots

μ, σ = 170, 10
d = Normal(μ, σ)

x = 130:0.1:210
pdf_values = pdf.(d, x)

plot(x, pdf_values, 
     lw=2, 
     legend=true,
     title="Distribuição Normal\n(μ = $μ, σ = $σ)",
     titlefontsize=11,
     xlabel="Altura (cm)",
     ylabel="Densidade de Probabilidade",
     grid=true,
     color=:steelblue,
     fillrange=0, 
     fillalpha=0.2,
     fillcolor=:cornflowerblue)

vline!([μ], lw=2, linestyle=:dash, color=:black, label="μ = $μ")
vline!([μ - σ, μ + σ], lw=1, linestyle=:dot, color=:red, label="±1σ")
vline!([μ - 2σ, μ + 2σ], lw=1, linestyle=:dot, color=:orange, label="±2σ")
vline!([μ - 3σ, μ + 3σ], lw=1, linestyle=:dot, color=:green, label="±3σ")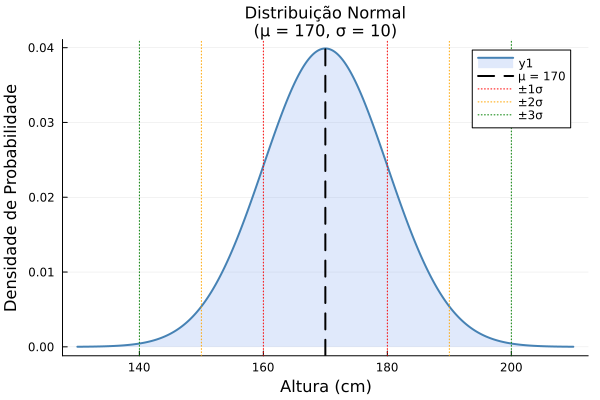

Distribuição Normal

Figura 4: Distribuição Normal com μ=170 e σ=10

2.2 Distribuição Exponencial

Modela o tempo entre eventos em um processo de Poisson.

Parâmetro

Função Densidade de Probabilidade

\(f(x) = \lambda e^{-\lambda x}, \text{ para } x \geq 0\)

Média e Variância

Aplicações

💡 Exemplo Prático
Tempo entre chegadas de clientes em um banco (λ = 0.5 clientes/minuto).
julia
using Distributions, Plots

# Parameter
λ = 0.5  
d = Exponential(1/λ)

# Values
x = 0:0.1:10
pdf_values = pdf.(d, x)

# Statistics
μ = mean(d)
med = quantile(d, 0.5)
σ² = var(d)  # Variance
σ = std(d)   # Standard deviation

# Create plot
plot(x, pdf_values, 
     linewidth=2, 
     legend=:topright,
     title="Distribuição Exponencial (λ = $λ)",
     xlabel="Tempo entre chegadas (min)",
     ylabel="Densidade de Probabilidade",
     grid=true,
     color=:steelblue,
     fillrange=0, 
     fillalpha=0.2,
     fillcolor=:lightblue,
     framestyle=:zerolines)

# Vertical lines for statistics
vline!([μ], linestyle=:dash, linewidth=2, color=:black, label="Média = $(round(μ, digits=2))")
vline!([med], linestyle=:dot, linewidth=2, color=:red, label="Mediana = $(round(med, digits=2))")
vline!([μ + σ], linestyle=:dashdot, linewidth=1.5, color=:green, label="μ + σ = $(round(μ+σ, digits=2))")

# Annotations
annotate!(μ, pdf(d, μ)+0.005, text("μ", :black, 10))
annotate!(med, pdf(d, med)+0.005, text("med", :red, 10))
annotate!(μ+σ, pdf(d, μ+σ)+0.005, text("μ+σ", :green, 10))

# Add variance information
annotate!(5, 0.25, 
          text("Estatísticas:\nMédia (μ) = 1/λ = $(round(μ, digits=2))\n" *
               "Variância (σ²) = 1/λ² = $(round(σ², digits=2))\n" *
               "Desvio Padrão (σ) = 1/λ = $(round(σ, digits=2))", 
               10, :left))

# Highlight important region
plot!(x, pdf_values, fillrange=0, fillalpha=0.3, fillcolor=:steelblue, 
      label="P(X ≤ $(round(μ, digits=2))) = $(round(cdf(d, μ), digits=2))")

# Add exponential formula
annotate!(7, 0.35, text("f(x) = λe^{-λx}", 12, :left))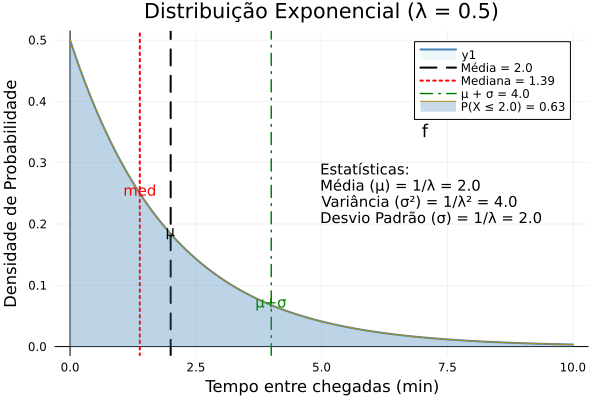

Distribuição Exponencial

Figura 3: Distribuição Exponencial com λ=0.5

2.3 Distribuição Uniforme Contínua

Todos os valores em um intervalo têm a mesma probabilidade de ocorrência.

Parâmetros

Função Densidade de Probabilidade

\(f(x) = \frac{1}{b-a}, \text{ para } a \leq x \leq b\)

Média e Variância

Aplicações

💡 Exemplo Prático
Geração de números aleatórios entre 0 e 1.
julia
using Distributions, Plots

# Parâmetros da distribuição uniforme
a, b = 0, 1

# Criando a distribuição
d = Uniform(a, b)

# Calculando Média e Variância
μ = mean(d)
σ² = var(d)

# Valores para o eixo x
x = -0.5:0.01:1.5

# Calculando a PDF
pdf_values = pdf.(d, x)

# Plotando PDF
plot(x, pdf_values, 
     lw=2, 
     legend=true,
     title="Distribuição Uniforme (a=$a, b=$b)",
     xlabel="Valor",
     ylabel="Densidade de Probabilidade",
     ylim=(0, 1.2),
     grid=true,
     color=:steelblue,
     fillrange=0, 
     fillalpha=0.2,
     fillcolor=:lightblue)

# Linhas verticais para limites, média
vline!([a], linestyle=:dash, color=:red, alpha=0.7, label="Limite a = $a")
vline!([b], linestyle=:dash, color=:orange, alpha=0.7, label="Limite b = $b")
vline!([μ], linestyle=:dashdot, color=:purple, alpha=0.8, lw=2, label="Média μ = $(round(μ, digits=2))")

# Linha horizontal da densidade constante
hline!([pdf(d, 0.5)], linestyle=:dot, color=:green, label="Densidade Constante = $(round(pdf(d, 0.5), digits=2))")

# Pontos destacados nos limites e média
scatter!([a, b, μ], [pdf(d, a), pdf(d, b), pdf(d, μ)], 
         markersize=7, 
         markercolor=:white, 
         markerstrokecolor=[:red, :orange, :purple], 
         markerstrokewidth=2, 
         label="")

# Anotações para a, b, média
annotate!([(a, -0.1, text("a = $a", :red, 10, :center)), 
           (b, -0.1, text("b = $b", :orange, 10, :center)),
           (μ, 0.05, text("μ = $(round(μ, digits=2))", :purple, 10, :center))])

# Texto para variância no gráfico
annotate!(0.5, 0.5, text("Variância σ² = $(round(σ², digits=3))", :black, 11))

plot!(legend=:topright)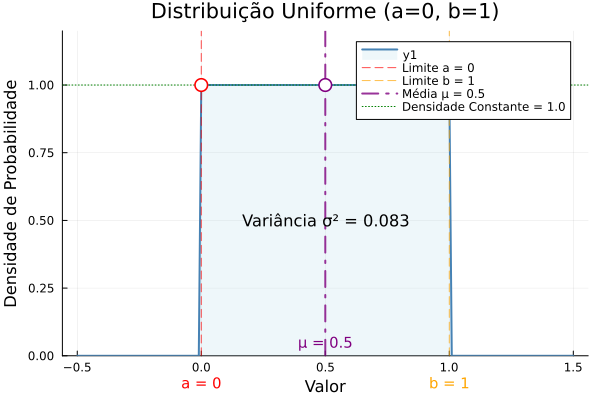

Distribuição Uniforme

Figura 5: Distribuição Uniforme contínua

3. Como Escolher a Distribuição Correta?

  1. Identifique o tipo de variável: Discreta ou contínua?
  2. Analise o domínio dos dados: Quais valores são possíveis?
  3. Verifique a forma dos dados: Simétricos, assimétricos, com caudas pesadas?
  4. Considere o fenômeno subjacente: Qual modelo teórico melhor se ajusta ao fenômeno?
  5. Use testes de adequação:
    • Teste Qui-quadrado
    • Teste de Kolmogorov-Smirnov
    • Teste de Anderson-Darling
    • Gráficos Q-Q
⚠️ Cuidado com Pressupostos!
A escolha incorreta da distribuição pode levar a conclusões equivocadas. Sempre valide os pressupostos antes de realizar inferências.

4. Aplicações Práticas

5. Aplicações Práticas

Engenharia

Finanças

Ciências Naturais

Ciências Sociais

Referências

  1. Bussab, W. O.; Morettin, P. A. Estatística Básica. 9ª ed. Saraiva, 2017.
  2. Montgomery, D. C.; Runger, G. C. Estatística Aplicada e Probabilidade para Engenheiros. 5ª ed. LTC, 2015.
  3. Magalhães, M. N.; Lima, A. C. P. Noções de Probabilidade e Estatística. 7ª ed. Edusp, 2013.
  4. Triola, M. F. Introdução à Estatística. 11ª ed. LTC, 2008.
  5. Devore, J. L. Probabilidade e Estatística para Engenharia e Ciências. 8ª ed. Cengage Learning, 2014.