A média aritmética é a medida de tendência central mais utilizada e conhecida. Ela representa o valor que mostra para onde os dados tendem a se agrupar, ou seja, o ponto de equilíbrio de um conjunto de valores.
A média aritmética de um conjunto de dados observados é igual à soma dos valores numéricos de cada observação, dividida pelo número total de observações.
Origem e História
O termo “aritmética” tem suas raízes no termo latino arithmetica, que deriva das palavras gregas ἀριθμός (arithmos), que significa número, e ἀριθμητική τέχνη (arithmetike tekhne), que significa a arte de contar.
A palavra “média” tem uma etimologia curiosa e multifacetada, enraizada tanto no comércio marítimo quanto na matemática. Sua origem remonta ao latim medieval avaria, termo usado no contexto das viagens comerciais marítimas no Mediterrâneo dos séculos XII e XIII para designar danos, perdas ou despesas extraordinárias sofridas durante uma travessia. Quando mercadorias precisavam ser descartadas ao mar para salvar o navio, os prejuízos eram distribuídos proporcionalmente entre todos os comerciantes envolvidos. Essa prática jurídica deu origem ao conceito de avaria grossa (general average, em inglês), onde cada parte contribuía com uma parte proporcional da perda.

Fórmula da Média Aritmética
A fórmula para calcular a média aritmética simples é:
\[\bar{x} = \frac{x_1 + x_2 + x_3 + \dots + x_n}{n} = \frac{\sum_{i=1}^{n} x_i}{n}\]Onde:
- $\bar{x}$ é a média aritmética
- $x_1, x_2, \dots, x_n$ são os valores do conjunto de dados
- $n$ é o número de elementos no conjunto
Em distribuições assimétricas, como a distribuição de renda ou de tempos de espera, a média pode não representar bem a tendência central.
Nestes casos, considere usar a mediana ou a moda, conforme o objetivo da análise estatística.
Exemplo Prático
Vamos calcular a média das notas de um aluno em cinco provas:
Exemplo em Julia
Aqui está como você pode calcular a média aritmética em Julia:
# Definindo as notas do aluno
notas = [7.5, 8.0, 6.5, 9.0, 7.0]
# Calculando a média usando a função mean() do pacote Statistics
using Statistics
media = mean(notas)
# Mostrando o resultado
println("As notas são: ", notas)
println("A média é: ", round(media, digits=2))Saída esperada:
Explicação do código:
- Criamos um vetor
notascom as cinco notas do aluno - Utilizamos a função
mean()do pacoteStatisticspara calcular a média - Exibimos as notas e o resultado da média
Você também pode calcular a média manualmente em Julia:
# Cálculo manual da média
soma = sum(notas)
quantidade = length(notas)
media_manual = soma / quantidade
println("Soma: ", soma)
println("Quantidade de notas: ", quantidade)
println("Média calculada manualmente: ", round(media_manual, digits=2))Dicas úteis:
- Certifique-se de que o pacote
Statisticsesteja carregado comusing Statistics - A função
mean()também funciona com arrays multidimensionais - Para dados muito grandes, considere usar
mean(skipmissing(dados))para lidar com valores ausentes
Vamos calcular a média das notas de um aluno em cinco provas:
| Prova | Nota |
|---|---|
| 1 | 7.5 |
| 2 | 8.0 |
| 3 | 6.5 |
| 4 | 9.0 |
| 5 | 8.5 |
Aplicando a fórmula:
\[\bar{x} = \frac{7.5 + 8.0 + 6.5 + 9.0 + 8.5}{5} = \frac{39.5}{5} = 7.9\]Portanto, a média do aluno é 7.9.
A média aritmética de um conjunto de dados observados é igual à soma dos valores numéricos de cada observação, dividida pelo número total de observações.
Em outras palavras, a média aritmética é o valor central de um conjunto de dados, calculado pela soma de todos os valores dividida pela quantidade de valores. Ela fornece uma medida simples da “tendência central” dos dados.
Em termos simples, a média é calculada somando-se todos os valores de um conjunto de dados e dividindo-se pelo número total de elementos.
Tipos de Média
Média Aritmética Simples
É a média convencional, onde todos os valores têm o mesmo peso no cálculo.
Exemplo: Para o conjunto {2, 4, 6, 8, 10}
Média = (2 + 4 + 6 + 8 + 10) ÷ 5 = 30 ÷ 5 = 6
Média Aritmética Ponderada
Neste tipo de média, cada valor tem um peso diferente no cálculo final.
\[\bar{x} = \frac{\sum_{i=1}^{n} x_i \cdot w_i}{\sum_{i=1}^{n} w_i}\]Onde $w_i$ representa o peso de cada valor.
Exemplo: Cálculo de média final com pesos diferentes para provas
Prova 1: nota 7,0 (peso 2)
Prova 2: nota 8,0 (peso 3)
Prova 3: nota 9,0 (peso 5)
Média Ponderada = (7×2 + 8×3 + 9×5) ÷ (2+3+5) = (14 + 24 + 45) ÷ 10 = 83 ÷ 10 = 8,3
Média Geométrica
A média geométrica é usada principalmente para conjuntos de valores positivos e para taxas de crescimento (como juros compostos, crescimento populacional, etc.).
\[M_g = \sqrt[n]{x_1 \cdot x_2 \cdot \ldots \cdot x_n}\]Exemplo: Para os valores 2, 8 e 32:
Média geométrica = $(2 \times 8 \times 32)^{1/3} = (512)^{1/3} = 8$
Nota: A média geométrica só é definida para números positivos.
Média Harmônica
A média harmônica é especialmente útil para médias de razões, como velocidade média em trajetos com diferentes velocidades.
\[M_h = \frac{n}{\sum_{i=1}^{n} \frac{1}{x_i}}\]Exemplo: Um carro percorre duas distâncias iguais a 60 km, uma a 30 km/h e outra a 60 km/h. Qual a velocidade média?
Média harmônica = $\frac{2}{\frac{1}{30} + \frac{1}{60}} = \frac{2}{\frac{2+1}{60}} = \frac{2}{\frac{3}{60}} = 40$ km/h
Nota: A média harmônica é sempre menor ou igual à média aritmética.
Média Quadrática (ou RMS)
A média quadrática é usada para medir a magnitude média de um conjunto de números, especialmente em física e engenharia (ex: corrente alternada).
\[M_q = \sqrt{\frac{1}{n}\sum_{i=1}^{n} x_i^2}\]Exemplo: Para os valores 3, 4 e 5:
Média quadrática = $\sqrt{\frac{3^2 + 4^2 + 5^2}{3}} = \sqrt{\frac{9+16+25}{3}} = \sqrt{\frac{50}{3}} \approx 4,08$
Nota: A média quadrática é sempre maior ou igual à média aritmética.
Média Móvel
A média móvel é uma ferramenta estatística utilizada para suavizar flutuações em séries temporais, facilitando a identificação de tendências ao longo do tempo. É muito utilizada em análise de dados financeiros, economia, meteorologia e controle de qualidade.
Definição:
A média móvel de ordem $k$ é calculada tirando a média dos últimos $k$ valores de uma série de dados, deslocando essa janela ao longo do tempo.
Fórmula:
\[MM_t = \frac{x_{t} + x_{t-1} + \ldots + x_{t-k+1}}{k}\]Onde:
- $MM_t$ = média móvel no tempo $t$
- $k$ = número de períodos da janela
- $x$ = valores da série
Exemplo:
Considere a série: 10, 12, 14, 16, 18, 20
Média móvel de ordem 3:
- 1ª média: (10 + 12 + 14) / 3 = 12
- 2ª média: (12 + 14 + 16) / 3 = 14
- 3ª média: (14 + 16 + 18) / 3 = 16
- 4ª média: (16 + 18 + 20) / 3 = 18
Portanto, a sequência de médias móveis é: 12, 14, 16, 18
Aplicações Comuns:
- Análise de tendências em séries financeiras (ex: preços de ações)
- Suavização de dados meteorológicos (ex: temperatura média)
- Controle de qualidade industrial
Nota: A escolha do valor de $k$ (tamanho da janela) afeta o quanto a série será suavizada: janelas maiores suavizam mais, mas podem atrasar a identificação de mudanças rápidas na tendência.
Resumo Visual
| Tipo | Fórmula Principal | Aplicação Comum |
|---|---|---|
| Aritmética Simples | $\bar{x} = \frac{\sum x_i}{n}$ | Dados gerais |
| Aritmética Ponderada | $\bar{x} = \frac{\sum x_i w_i}{\sum w_i}$ | Notas, médias com pesos |
| Geométrica | $M_g = \sqrt[n]{x_1 x_2 … x_n}$ | Crescimento, taxas |
| Harmônica | $M_h = \frac{n}{\sum \frac{1}{x_i}}$ | Razões, velocidades médias |
| Quadrática (RMS) | $M_q = \sqrt{\frac{1}{n}\sum x_i^2}$ | Física, engenharia |
Propriedades da Média
- Influência de valores extremos: A média é sensível a valores extremos (outliers). Um valor muito alto ou muito baixo pode distorcer significativamente o resultado.
- Representatividade: A média nem sempre representa bem um conjunto de dados com distribuição assimétrica.
- Unicidade: Para um conjunto de dados, existe apenas uma média aritmética.
- Valor intermediário: A média sempre está entre o valor mínimo e o valor máximo do conjunto.
Limitações da Média
Embora seja uma medida amplamente utilizada, a média apresenta algumas limitações:
- É fortemente influenciada por valores extremos (outliers)
- Não representa bem conjuntos com distribuição assimétrica
- Pode resultar em um valor que não existe no conjunto original
- Não fornece informações sobre a dispersão dos dados
Por isso, é importante considerar outras medidas de tendência central, como a mediana e a moda, para uma análise mais completa.
Notas Importantes
- Sempre escolha o tipo de média mais adequado ao contexto do problema.
- A média aritmética pode ser enganosa em dados com muitos extremos (outliers).
- A média geométrica não é adequada para valores negativos ou zero.
- A média harmônica é ideal para médias de taxas (ex: velocidade, produtividade).
- A média quadrática é útil quando se deseja dar mais peso a valores maiores.
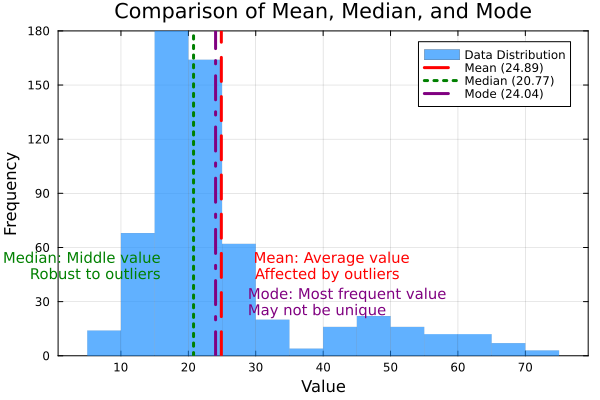
A média é puxada na direção dos valores extremos (cauda), enquanto a mediana representa o valor central e a moda indica o valor mais frequente.
Curiosidade
- Para dois valores positivos quaisquer: Média harmônica ≤ Média geométrica ≤ Média aritmética ≤ Média quadrática.
- Esse resultado é conhecido como desigualdade das médias.
Calculadora de Média
Calcule a média aritmética
Insira os valores separados por vírgula:
Média: -
